 Maybe I'm missing their point.
Maybe I'm missing their point.
Posted on 04/09/2023 10:31:05 AM PDT by Twotone
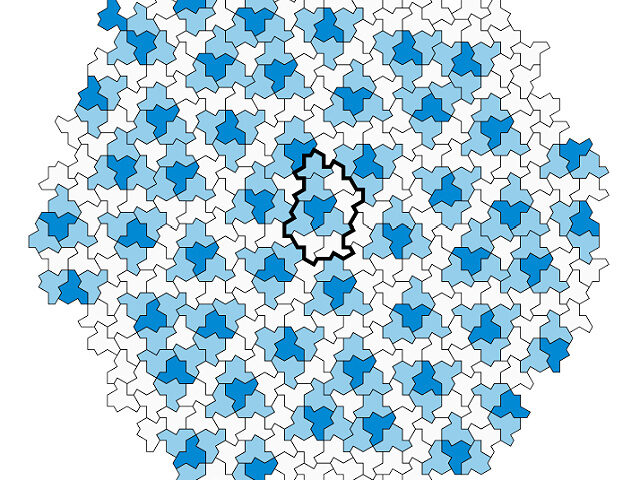
An amateur mathematician in the United Kingdom may have solved a 60-year-old problem in geometry, garnering the attention of researchers.
CNN reported David Smith, a retired printing technician, has discovered a shape known as an “einstein,” which can be tiled over a surface without the pattern repeating. The outlet noted mathematicians first began working on this problem in the 1960s.
Smith and three coauthors, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss, published a paper explaining Smith’s finding.
Smith, who says he is “always looking for an interesting shape,” wrote a blog post to serve as a “scrapbook” of his experiments with non-repeating tiles in which he thanked his three coauthors for the “super human effort” they expended helping him make his work public.
Live Science reported that mathematicians have long debated whether such shapes could even exist and, if so, what form they might take:
For decades, mathematicians wondered if it was possible to find a single special shape that could perfectly tile a surface, without leaving any gaps or causing any overlaps, with the pattern never repeating. Of course, this is trivial to do with a pattern that repeats — just look at a bathroom or kitchen floor, which is probably made up of simple rectangular tiles. If you were to pick up your floor and move it (called a “translation” in mathematics), you could find a position where the floor looks exactly the same as before, proving that it’s a repeating pattern.
Stanford Professor Rafe Mazzeo observed that Smith’s finding could have applications in physics, chemistry, and other fields, per CNN.
“This new discovery is a strikingly simple example. There are no standard techniques known for finding new aperiodic tiles, so this involved a really new idea. That is always exciting,” he said.
(Excerpt) Read more at breitbart.com ...
Math is racist, hang him.
Pretty brilliant.
 Maybe I'm missing their point.
Maybe I'm missing their point.

Looks like a complex variant of the “Cairo Grid.” A kind of tessalation using a five-sided shape.
That’s likely an extremely rigid structural design because it wouldn’t slip along fault planes. A 3D version would be a mind blower.
If you take that whole pattern and translate a transparent copy of it over the original (shift it to the side, rotate it etc.), you won’t be able to get it to match up.
Very interesting. Penrose tiling is also aperiodic but requires at least two different tile shapes. I wonder when these new tiles will be commercially available.
Sort of like Penrose tiling?
13 sided shape.
The Penrose tiling uses two different shapes. This is just one shape.
I don’t understand the problem well enough to understand why this is a problem.
Am I alone on this?
Geometry has always been a mystery to me.
Most shapes that are able to completely cover an area with no gaps result in patterns that are periodic, i.e. that repeat themselves perfectly over and over. For example, an array of squares, triangle or hexagons, can cover a surface with no gaps, but if you make a transparency of the pattern, this pattern can be moved over by one tile or two or three, or rotated by different angles, and still overlap perfectly with what it was before the translation or rotation. Being able to cover a surface with only two different shapes (the Penrose tiling) or with only one shape (the shape in this article) with no gaps, but without ever repeating, is rare. According to the article, it wasn’t even known if it was possible to use one single shape to completely cover a plane with no gaps and without any periodic repetition.
“I don’t understand the problem well enough to understand why this is a problem.
Am I alone on this?”
No. I don’t get it. And I guess I lack imagination because for me, I wonder why anyone has been thinking about this since the 60s.
Did he do Penrose tiles one better?
https://en.wikipedia.org/wiki/Penrose_tiling
https://en.wikipedia.org/wiki/List_of_aperiodic_sets_of_tiles
It would be interesting to see how they proved it doesn’t repeat. Maybe after laying down a spread a billion wide or so it does.
I probably wouldn’t follow the proof anyway.

It makes better sense if you hold it up to a mirror and blink your eyes real fast...
Disclaimer: Opinions posted on Free Republic are those of the individual posters and do not necessarily represent the opinion of Free Republic or its management. All materials posted herein are protected by copyright law and the exemption for fair use of copyrighted works.