Skip to comments.
Ancient Navigators Could Have Measured Longitude -- in Egypt in 232 B.C. !
21st Century: Science and Technology Magazine ^
| Fall 2001
| Rick Sanders
Posted on 01/12/2003 11:19:24 AM PST by ex-Texan
Ancient Navigators Could Have Measured Longitude -- in Egypt in 232 B.C. !
by Rick Sanders
Around the year 232 B.C., Captain Rata and Navigator Maui set out with a flotilla of ships from Egypt in an attempt to circumnavigate the Earth. On the night of August 6-7, 2001, between the hours of 11 PM and 3 AM, this writer, and fellow amateur astronomer Bert Cooper, proved in principle that Captain Rata and Navigator Maui could have known and charted their location, by longitude, most of the time during that voyage.
The Maui expedition was under the guidance of Eratosthenes, the great scientist who was also the chief librarian of the library at Alexandria. Could this voyage have demonstrated Eratosthenes' theorem that the world was round, and measured approximately 24,500 miles in circumference? One of the navigational instruments which Maui had with him was a strange looking "calculator" that he called a tanawa; such an instrument was known, in 1492, as a torquetum.
Intrigued by a photograph of the cave drawing of that tanawa in Irian Jaya, western New Guinea, I speculated that Maui must have been looking at the ecliptic to measure "lunar distance," in order to find his longitude. Maui's tanawa was of such importance, that he drew it on the cave wall with the inscription, deciphered in the 1970s by epigrapher Barry Fell: "The Earth is tilted. Therefore, the signs of half of the ecliptic watch over the south, the other (half) rise in the ascendant. This is the calculator of Maui."
Eratosthenes had just measured the circumference of the Earth, and the circumference of a sphere is the same in all directions. We know that Maui was thinking about this, because his cave drawings also include a proof of Eratosthenes' experiment to measure the Earth's circumference.
To test the hypotheses, we built a wooden torquetum and used a simplified version of it to measure the change in angular distance between the Moon and the star Altair, in the constellation Aquila (the Eagle). This success proves official dogma wrong, and proves that, in principle, Navigator Maui, during his voyage could have used tables brought from Alexandria, drawn up by Eratosthenes or his collaborators, compared those lunar distances with the distances that he measured, and come up with a good estimate of his longitude.
It is important to note that we are not claiming here that we know everything about the torquetum. We simplified our device for the proof-of-principle experiment, but we will carry out and report on more experiments, using the full instrument.
The torquetum's value, as an analogue calculator, must have been immense, because, once a planet or the Moon are not on the meridian, all "straight lines" become curves—so that calculations are difficult, even with a modern calculator. However, the 23.5-degree plane on the torquetum allows one to directly read the longitude and latitude of a planet or the Moon, relative to the ecliptic, without calculation. These data would be invaluable for predicting eclipses and occultations of various stars or planets by the Moon.
The Inspiration for the Experiment
This was intriguing! What was this "tanawa" for? Why the 23.5-degree plane, characteristic of the torquetum? It could only mean that Maui was looking at the ecliptic, the Moon, and the planets, the "wandering stars."
Of the two torquetums surviving in the world, one belonged to Nicholas of Cusa, and the other to Regiomontanus, both of whom were involved in calendar reform, including setting the date of Easter, which, along with some other religious festivals, is dated by the interaction of the lunar and solar calendars.
But what could Maui have been doing? Trying to determine longitude? The very thought was heretical. To take things out of the realm of speculation, the only solution was to build a torquetum, and see if longitude could be determined by using sightings of the Moon, with simple backyard equipment; if this succeeded, then Navigator Maui could have also succeeded.
PROBABLE ROUTE OF THE EGYPTIAN VOYAGE IN 232 B.C.
Deciphered rock and cave inscriptions from the Pacific islands, western New Guinea, and Santiago, Chile, tell of an Egyptian flotilla that set sail around 232 B.C., during the reign of Ptolemy III, on a mission to circumnavigate the globe. The six ships sailed under the direction of Captain Rata and Navigator Maui, a friend of the astronomer Eratosthenes (ca. 275-194 B.C.), who headed the famous library at Alexandria. Maui's inscriptions, as deciphered in the 1970s by epigrapher Barry Fell, indicated that this was a proof-of-principle voyage, to demonstrate Eratosthenes' theorem that the world was round, and approximately 24,500 miles in circumference.
Finding Longitude
You cannot tell longitude from the stars alone, because their daily motion is purely apparent, caused by the rotation of the Earth. At 8 PM (solar apparent time), any star, seen from anywhere, whether Ferrara, Paris, or Cairo, will have the same azimuth as it does in Washington, D.C., Chicago, Sioux Falls, S.D., Seattle, or anywhere else. The Moon shares in this apparent motion to the west, but it also has its own independent, real motion.
Look at what Amerigo Vespucci, himself at the frontiers of post-Dark-Ages navigational astronomy, said of this in 1502, in Letter IV:
". . . I maintain that I learned [my longitude] . . . by the eclipses and conjunctions of the Moon with the planets; and I have lost many nights of sleep in reconciling my calculations with the precepts of those sages who have devised the manuals and written of the movements, conjunctions, aspects, and eclipses of the two luminaries and of the wandering stars, such as the wise King Don Alfonso in his Tables, Johannes Regiomontanus in his Almanac, and Blanchinus, and the Rabbi Zacuto in his almanac, which is perpetual; and these were composed in different meridians: King Don Alfonso's book in the meridian of Toledo, and Johannes Regiomontanus's in that of Ferrara, and the other two in that of Salamanca."2 The best "clock" to use for reference, is the stars. In the roughly 27.3 solar days of a lunar orbit, the Moon moves a full 360 degrees around the sky, returning to its old position among the stars. This is 13 degrees per day, or just over 0.5 degree per hour. So, while the rotation of the Earth causes the stars and the Moon to appear to move from east to west across the night sky, the Moon, because of its own orbit around the Earth, fights back against this apparent motion, and seems to move eastward (or retrograde) by about 0.5 degree per hour. In other words, the Moon "moves" west only 11.5 degrees per hour.
A brass model of Maui's tanawa, constructed by Dr. Sentiel Rommel. The base (A) in the plane of the observer's horizon, is oriented so that the axis of symmetry is parallel to the meridian. (B) is the equatorial plane. (C) is the ecliptic plane (viewed from one side in Maui's drawing, hence appearing as a line). Drawing by Matt Makowski in The Epigraphic Society Occasional Publications, Vol. 32, No. 29, Feb. 1975
Thus, if a known star is in a given position on the celestial sphere (measured by azimuth and right ascension), a table could be drawn up at a given location for each night, showing how distant the Moon appears to be from that star.
For example: If a ship sailed west out of a port, and its new longitude were now 15 degrees west (one hour) of that port, and those on the ship could see the Moon and the reference star, the Moon would appear to be 0.5 degree east of where the table would show it to be for the port of departure. There is nothing here that navigator Maui in 232 B.C. could not have known. The only question would be whether his instruments could measure an angular difference on the order of 0.5 degree.
Our Observations
Our observational experiment showed that a simplified torquetum could do it. In the time that Altair had moved 41.8 degrees west along the equatorial plane, the Moon had moved only 40.25 degrees, a difference of 1.55 degrees. Because the Moon should retrograde about 0.5 degree/hour, the calculated regression would equal 1.39 degrees. This error of less than 1/6th (or 0.166) of a degree is well within our instrument limitations, which can be read only to 0.25 of a degree.
-------------------------------------------------------- Notes: 1. For the story of the Rata-Maui Expedition, see "The Decipherment and Discovery of a Voyage to America in 232 B.C.," by Marjorie Mazel Hecht, 21st Century, Winter 1998-1999, p. 62; "Indian Inscriptions from the Cordilleras in Chile" found by Karl Stolp in 1885, 21st Century, Winter 1998-1999, p. 66; "On Eratosthenes, Maui's Voyage of Discovery, and Reviving the Principle of Discovery Today," by Lyndon H. LaRouche, Jr., 21st Century, Spring 1999, p. 24; "Eratosthenes' Instruments Guided Maui's 3rd Century B.C. Voyage," by Marjorie Mazel Hecht, 21st Century, Spring 1999, p. 74; and "Maui's Tanawa: A Torquetum of 232 B.C.," by Sentiel Rommel, Ph.D., 21st Century, Spring 1999, p. 75.
2. Cited in Letters From A New World, 1992. Ed. Luciano Formisano (New York: Marsilio Publishers), pp. 38-39.
21st Century, P.O. Box 16285, Washington, D.C. 20041
www.21stcenturysciencetech.com
Copyright © 2003 21st Century Science Associates. All rights reserved.
(Excerpt) Read more at 21stcenturysciencetech.com ...
TOPICS: Culture/Society; Extended News; Foreign Affairs
KEYWORDS: ancientnavigation; archaeology; earthisround; egypt; egyptin232bc; ggg; godsgravesglyphs; heyerdahl; history; navigation; precolumbiantrade; ricksanders; thorheyerdahl
Navigation: use the links below to view more comments.
first previous 1-20, 21-40, 41-60, 61-80 ... 101-103 next last
To: White Mountain; CubicleGuy; Utah Girl; pseudogratix; rising tide; Grig; Edward Watson; Illbay
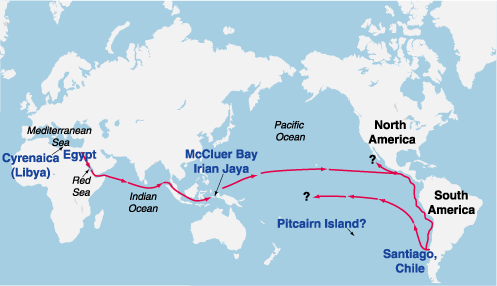
Figure 1 PROBABLE ROUTE OF THE EGYPTIAN VOYAGE IN 232 B.C. Deciphered rock and cave inscriptions from the Pacific islands, western New Guinea, and Santiago, Chile, tell of an Egyptian flotilla that set sail around 232 B.C., during the reign of Ptolemy III, on a mission to circumnavigate the globe. The six ships sailed under the direction of Captain Rata and Navigator Maui, a friend of the astronomer Eratosthenes (ca. 275-194 B.C.), who headed the famous library at Alexandria. Maui's inscriptions, as deciphered in the 1970s by epigrapher Barry Fell, indicated that this was a proof-of-principle voyage, to demonstrate Eratosthenes' theorem that the world was round, and approximately 24,500 miles in circumference.
41
posted on
01/12/2003 6:59:47 PM PST
by
restornu
(LooK Up!)
To: Vast Buffalo Wing Conspiracy
I'm a FReeper and I know something about history.
I know that islam carried on a lot of Greek/Hellenistic science without improving on it.
Until the Iranian muslim Al-Ghazzali (1058-1111) told his people to turn their back on science and philosophy. He instructed them to concentrate only on their religion.
Following his advice, the khalifah burnt the library of Baghdad in 1150.
At the same time, Saint Thomas (1225-74) told the West that science and Christianity were not in conflict.
He even argued that Aristotle was a kind of pre-Christian saint.
Science does shake belief in God and make people question religion. But not all religions choose to quake at the sight of it and turn their back on progress.
The greatest example of fine machinery up until modern times was the mechanical clock, which was invented by monks in monasteries.
The West has been shaped by Christian values and has led the world in technological achievements. It would be great if some other religions would quit holding their cultures hostage in a self-imposed Dark Age and quit blaming their troubles on the West.
Just for the record, the nose of the Sphinx was not destroyed by Napoleon's troops but by a muslim (or sufi if you prefer) around 1300 A.D. who thought it was idolaritous.
While all cultures have engaged in artistic vandalism, a religion that hates representational images of any kind, is likely to do more than their share.
Long live Charles Martel!
42
posted on
01/12/2003 7:01:36 PM PST
by
Arkady
To: RightWhale
Who was involved in the civil war?
Not Christians. That came later, after Constantine.
The museum and library survived for many centuries but were destroyed in the civil war that occurred under the Roman emperor Aurelian in the late 3rd century AD....
In the East, [Aurelian] defeated Zenobia's troops easily and occupied Palmyra in 272. Shortly afterward, an uprising broke out in Egypt under the instigation of a rich merchant, who, like a great part of the population, was a partisan of the Palmyrene queen.In response, Aurelian undertook a second campaign, plundering Palmyra and subjugating Alexandria. These troubles, however, along with the devastation of the great caravan city, were to set back Roman trade seriously in the East. Later, rounding back on the Gallic empire of Postumus' successors, he easily defeated Tetricus , a peaceful man not very willing to fight, near Cabillonum. The unity of the empire was restored, and Aurelian celebrated a splendid triumph in Rome. He also reestablished discipline in the state, sternly quelled a riot of artisans in the mints of Rome, organized the provisioning of the city by militarizing several corporations (the bakers, the pork merchants), and tried to stop the inflation by minting an antoninianus of sounder value. His religious policy was original: in order to strengthen the moral unity of the empire and his own power, he declared himself to be the protégé of the Sol Invictus (the Invincible Sun) and built a magnificent temple for this god with the Palmyrene spoils. Aurelian was also sometimes officially called dominus et deus: the principate had definitely been succeeded by the “dominate.” In 275 Aurelian was murdered by certain officers who mistakenly believed that their lives were in danger.
--Encyclopedia Britannica
43
posted on
01/12/2003 7:25:55 PM PST
by
aruanan
To: restornu; Wrigley; Elsie
But you believe they were Jews (that spoke a unknown dialect of Egyptian..that could not be the language decipered here as no one but joseph Smith could read it ) not Egyptians..you can't have it both ways rest this does not help you much:>)
44
posted on
01/12/2003 7:29:54 PM PST
by
RnMomof7
(Eph 2:8 For by grace are ye saved through faith; and that not of yourselves: [it is] the gift of God)
To: Vast Buffalo Wing Conspiracy
All you gloaters are the same in every age: ignorant fools, taking credit for things not of your own doing, living off the seed corn that was laid in store by your more energetic and foresighted ancestors. If I have seen further than other men, it was because I was standing on their glasses....
(No, I didn't make that up. Don't remember the proper attribution.)
45
posted on
01/12/2003 7:44:02 PM PST
by
thulldud
To: ex-Texan
Bump
46
posted on
01/12/2003 7:51:09 PM PST
by
Fiddlstix
(Wanted: Used "Tag Lines" in good condition. Top prices paid for Quality. Inquire Within.)
To: lds23
What, the sky?
Sorry, couldn't resist. :)
47
posted on
01/12/2003 8:00:06 PM PST
by
altayann
To: Experiment 6-2-6
Longitude IS a great book and I give them as gifts as I bought several first editions.
My son gave me the book "ZERO" The Biography of a Dangerous Idea, by Charles Seife.
Try it, you'll like it!!
To: lds23
"I have this strange feeling that those pyramids are pointing to something really, really important."
The unusual location of the Great Pyramid suggests that it was the monument spoken of in Scripture by Isaiah the prophet.
Isaiah 19:19-20
"In that day shall thee be an altar to the Lord in the midst of the land of Egypt, and a pillar Hebrew "Matstsebah" correctly translated means monument) at the border thereof to the Lord. And it shall be for a sign, and for a witness unto the Lord of HOsts in the land of Egypt."
Since the full official name of the Pyramind, the Great Pyramid of Giza, means, in English, the Great Pyramid of the Border, the answer to the apparently contradictory definition of Isaiah is found in the Great Pyramid. The only spot on the face of the earth that completely answers this description, both geometrically and geographically, is the precise place where the Great Pyramid actually stands."
Page 13, "The Great Pyramid Decoded", E. Raymond Capt
49
posted on
01/12/2003 8:16:11 PM PST
by
Spirited
To: Arkady
Long live Charles Martel! Wow, that's a reference you don't hear that often. I've long considered Tours to be the most significant turning event in western culture. Most folks don't even know what it is. Just imagine what the world would be like without the hammer.
To: ex-Texan
Bump for later reading
51
posted on
01/12/2003 8:49:28 PM PST
by
Orion78
(I hope Golitsyn is wrong)
To: T. P. Pole
52
posted on
01/12/2003 9:47:41 PM PST
by
ex-Texan
To: yankeedame
Oh, good grief! No one "destroyed" Egypt and/or its skills and knowledge. It didn't ended like a brick through a plate glass window; ... No, it ended when the last Librarian of Alexandria was dragged from her chariot by a screaming mob of fanatics, had the flesh scraped from her bones by oyster shells, was then dismembered and, so it is said, her remains were partially eaten, and the rest burned.
Hypatia of Alexandria, 415 AD.
To: ex-Texan
BTTT for a later read
54
posted on
01/12/2003 11:08:48 PM PST
by
Mr_Magoo
(Single, Available, and Easy)
To: Arkady
The greatest example of fine machinery up until modern times was the mechanical clock, which was invented by monks in monasteries. Nope: by Ctesibios of Alexandria in about 618 AUC (135 BC). Pagan Greek, of course.
The "pendulum clock" as we know it today was invented by Christiaan Huygens in 1656. The clocks used by monks were typical Dark Age technology, which is to say inferior to their predecessors in Antiquity and their sucessors in modern times. The only significant improvement in a thousand years was the verge escapement, developed in the late fourteenth century, and almost certainly not by monks, since of the three English clock makers whose names have survived from that period, all were lay people.
To: ex-Texan
Equatorial-torquetum

56
posted on
01/12/2003 11:21:17 PM PST
by
Consort
To: Spirited
Since the full official name of the Pyramind, the Great Pyramid of Giza, means, in English, the Great Pyramid of the Border I'd appreciate a reference to that. My sources say the Pyramid of Cheops was called akhet khufu, which means, unsurprisingly, "pyramid of cheops". The Egyptian word for pyramid is derived from their word for "horizon", not "border". It's a religious metaphor but the explanation is a bit long.
To: ex-Texan
Time, I guess, for a post that addresses the main topic. Could the Ancients determine longitude, and if so, how?
Please note that I regard the "expedition" as fantasy, it is the engineering that interests me.
First, it is almost certain that the Hellenistic Age did know how to measure longitude, because we have maps that prove it. Or, at least, copies of those maps. The most famous - or infamous - is probably the Piri Reis map discussed in Charles Hapgood's fascinating book Maps of the Ancient Sea Kings, but there are better examples.
The Dulcert Portolano of 1339 is in my opinion the best, because it contains fewer copying errors than most, mesured by islands, rivers, estuaries etc. It could not have been produced in the Middle Ages - their idea of a map is the Mappa mundi in Hereford Cathedral, 1289 or so.
So an earlier civilization drew the original portolano, which is further indicated by some features of the map, for example the Guadalquivir is shown with an estuary, as it was in Greek times, rather than a delta. I don't buy Hapgood's thesis that the map makers came from Atlantis, so that leaves the Ancients.
Now, the average error in longitude on the Dulcert Portolano is about 45 minutes arc, three quarters of a degree, or at that latitude about 40 nautical miles. Good enough for point-to-point navigation.
So yes, they did it. But how?
Not with a marine chronometer, that's also pretty certain. No such device is described in the texts, and all we know of ancient clocks says they could not have kept accurate time on a moving vessel. That had to wait until Harrison's time.
That leaves a natural clock, and the obvious first choice is the moon. Would it work?
The math is simple. The moon revolves once around the Earth in 30 days, which is 12 degrees a day or 30 minutes arc an hour. The Earth rotates once in 24 hours, which is 15 degrees an hour or one degree in 4 minutes.
Therefore, to measure longitude accurate to one degree, you need to measure time accurate to 4 minutes. If you are measuring time by tracking the moon against the fixed stars, well, in 4 minutes it moves just 2 minutes arc, one-thirtieth of a degree, or, if you prefer, just one-fifteenth of its own diameter.
Could you do that with naked-eye observation? Absolutely not. Working with the largest and best astronomical instruments ever built, at Uraniborg on the island of Hveen, the great Tycho de Brahe could achieve only half that accuracy.
So you need a faster-running clock, or a telescope, or both. From Heron of Alexandria's Catoptrica, we know the Ancients understood enough of the science of optics to build telescopes, and from Herodotus we have mention of an instrument that sounds very like a telescope, but alas there is no direct proof or "smoking tube".
And if you have a telescope, you will find in the sky as fine a clock as you would ever need: the Galilean satellites of Jupiter. That's my best guess as to how they did it.
To: Arkady
Long live Charles Martel!
Yes!
Good post
To: T. P. Pole
Yes, it is a reference that needs to made more often. One of the most important battles (if not the most important battle) in the last two thousand years. It is also more proof that islam has been violent since its invention.
Navigation: use the links below to view more comments.
first previous 1-20, 21-40, 41-60, 61-80 ... 101-103 next last
Disclaimer:
Opinions posted on Free Republic are those of the individual
posters and do not necessarily represent the opinion of Free Republic or its
management. All materials posted herein are protected by copyright law and the
exemption for fair use of copyrighted works.
FreeRepublic.com is powered by software copyright 2000-2008 John Robinson

