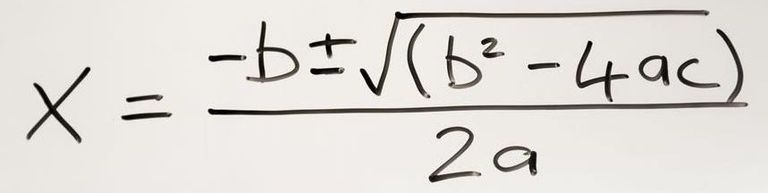
Posted on 12/09/2019 10:17:36 AM PST by Red Badger
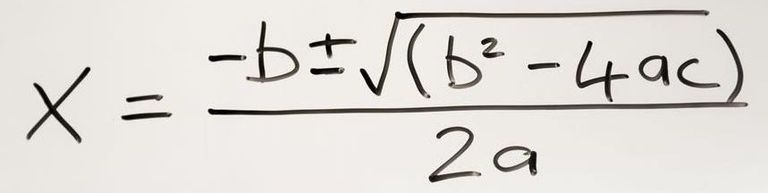
A mathematician at Carnegie Mellon University has developed an easier way to solve quadratic equations.
The mathematician hopes this method will help students avoid memorizing obtuse formulas.
His secret is in generalizing two roots together instead of keeping them as separate values.
==========================================================================
A mathematician has derived an easier way to solve quadratic equation problems, according to MIT's Technology Review. Quadratic equations are polynomials that include an x², and teachers use them to teach students to find two solutions at once. The new process, developed by Dr. Po-Shen Loh at Carnegie Mellon University, goes around traditional methods like completing the square and turns finding roots into a simpler thing involving fewer steps that are also more intuitive. Here's Dr. Loh's explainer video.
VIDEO AT LINK
Quadratic equations fall into an interesting donut hole in education. Students learn them beginning in algebra or pre-algebra classes, but they’re spoonfed examples that work out very easily and with whole integer solutions. The same thing happens with the Pythagorean theorem, where in school, most examples end up solving out to Pythagorean triples, the small set of integer values that work cleanly into the Pythagorean theorem.
Quadratic equations are polynomials, meaning strings of math terms. An expression like “x + 4” is a polynomial. They can have one or many variables in any combination, and the magnitude of them is decided by what power the variables are taken to. So x + 4 is an expression describing a straight line, but (x + 4)² is a curve. Since a line crosses just once through any particular latitude or longitude, its solution is just one value. If you have x², that means two root values, in a shape like a circle or arc that makes two crossings.
Dr. Loh’s method, which he also shared in detail on his website, uses the idea of the two roots of every quadratic equation to make a simpler way to derive those roots. He realized he could describe the two roots of a quadratic equation this way: Combined, they average out to a certain value, then there’s a value z that shows any additional unknown value. Instead of searching for two separate, different values, we’re searching for two identical values to begin with. This simplifies the arithmetic part of multiplying the formula out.
Dr. Loh believes students can learn this method more intuitively, partly because there’s not a special, separate formula required. If students can remember some simple generalizations about roots, they can decide where to go next. It’s still complicated, but it’s less complicated, especially if Dr. Loh is right that this will smooth students’s understanding of how quadratic equations work and how they fit into math. Understanding them is key to the beginning ideas of precalculus, for example.
Outside of classroom-ready examples, the quadratic method isn't simple. Real examples and applications are messy, with ugly roots made of decimals or irrational numbers. As a student, it's hard to know you've found the right answer. Dr. Loh’s new method is for real life, but he hopes it will also help students feel they understand the quadratic formula better at the same time. Many math students struggle to move across the gulf in understanding between simple classroom examples and applying ideas themselves, and Dr. Loh wants to build them a better bridge.
I agree. its not new unless you are a self centered millennial who thinks that everything started when you were born. I met one who said she liked classic rock, I mentioned I liked deep purple and she said “ who?”. typical. shfh
If you looked at the answers, there would be two pairs, varying in sign. Pick the painfully obvious pair, and check the sign.
Always got a kick out of the proctor coming over when I’d finished, and saying I had time to check my answers. “I did.”
Quadratic equations say common core is no such thing.
Two of the ‘answers’ were always WAAAAAAAY OFF!...... so then you were 1:2....................
He acknowledges that it’s not new, and is hundreds of years old. But it’s a new way to teach solving quadratics without the quadratic formula. For people who have trouble memorizing, this might be preferable.
I saved time in high school by skipping those math classes. Turns out I was right and my parents were wrong, it was useless information that I would never need. My argument was useless at the time.......
It is an easier way. but yiu have to have some bright peolple to teach them a concept , most people need a step by step fromula to do math. they cant just see 13x12 =13x13 -(13). or 169-13 or 156. they have to break it down, (3x1)+(3x10)+(10x1). etc.. . etc.. I was at 169-13 when i wrote the problem
It is an easier way. but yiu have to have some bright peolple to teach them a concept , most people need a step by step fromula to do math. they cant just see 13x12 =13x13 -(13). or 169-13 or 156. they have to break it down, (3x1)+(3x10)+(10x1). etc.. . etc.. I was at 169-13 when i wrote the problem
The Algebra textbooks I had in the late ‘70s/early ‘80s show this method as an explanation of the quadratic formula. Of course, those textbooks were written before Carter’s Department of Education was created...
Bump for later...
Wow...looks like he re-discovered Descartes!
...oh René Descartes was a drunken fart ..
...I drink therefore I am!
Furthermore, the technique demonstrated applies only to the special case of quadratics where a=1. If you add in the complication of a<>1, although I haven't tried to apply this new method, you are going to have more complicated expressions and you might as well have started with the general solution to begin with.
Meth cooking at MIT reaches new levels...
Not necessary.....
I guess I live a sheltered life. I can't remember the last time, in the course of my day to day activities, when I've been asked to solve an quadratic equation.
I have kids telling me they learned this last year.
I’m surprised!.......................That they still teach QE!.....................
You can always make a=1, you just divide both sides by a. Since the other side is 0, it really doesn’t matter.
But having not had time to watch his video, I’m still trying to figure out why the general quadratic equation is considered “hard to understand”.
The article shows the old way with a single equation. If the new way is so easy, why doesn’t the article describe how to do it? Minus b plus and minus the square root of b squared minus four a c all over 2a can be performed in less than a minute with a calculator to do the square root and described in a single sentence. The new method requires you to watch a video??? Every time?
Disclaimer: Opinions posted on Free Republic are those of the individual posters and do not necessarily represent the opinion of Free Republic or its management. All materials posted herein are protected by copyright law and the exemption for fair use of copyrighted works.