Posted on 06/29/2016 8:33:17 PM PDT by MtnClimber
In 2012, Mathematician Ian Stewart came out with an excellent and deeply researched book titled "In Pursuit of the Unknown: 17 Equations That Changed the World."
His book takes a look at the most pivotal equations of all time, and puts them in a human, rather than technical context.
"Equations definitely can be dull, and they can seem complicated, but that’s because they are often presented in a dull and complicated way," Stewart told Business Insider. "I have an advantage over school math teachers: I'm not trying to show you how to do the sums yourself." ...
Stewart continued that "equations are a vital part of our culture. The stories behind them — the people who discovered or invented them and the periods in which they lived — are fascinating."
Here are 17 equations that have changed the world:
The Pythagorean Theorem
Image: Business Insider What does it mean? The square of the hypotenuse of a right triangle is equal to the sum of the squares of its legs.
History: Though attributed to Pythagoras, it is not certain that he was the first person to prove it. The first clear proof came from Euclid, and it is possible the concept was known 1,000 years before Pythoragas by the Babylonians.
Importance: The equation is at the core of much of geometry, links it with algebra, and is the foundation of trigonometry. Without it, accurate surveying, mapmaking, and navigation would be impossible.
In terms of pure math, the Pythagorean Theorem defines normal, Euclidean plane geometry. For example, a right triangle drawn on the surface of a sphere like the Earth doesn't necessarily satisfy the theorem.
Modern use: Triangulation is used to this day to pinpoint relative location for GPS navigation.
(Excerpt) Read more at weforum.org ...
1 + 2 + 3 + 4 + 5 + ... = -1/12
Supposedly this is a key to understanding String Theory
Also a key to understanding why everything is so totally messed up today ... even down to the math.
Maxwell’s Equations were in the list.
They are!
Why not just read the article. It is interesting.
++++
LOL. What??? You want me to break with a well established Freeper tradition?
Actually I thought it would be more fun to make my own list. After looking at the list I’m thinking I did pretty good. I should have put in the a squared plus b squared equals c squared bit and the basic definition of differential calculus.
And it’s a good thing they are. I was ready to call my lawyer if they were left out.
Yeah! What’s with all those uppity white people and that numbers stuff?/
marriage = kids + pool + house - money^2 -sex^3
The big question used to be, “Do the solutions of the Navier-Stokes equation include turbulence?”
Surely this must have been resolved by now! But I haven’t heard.
... heh. The Wikipedia article on Navier-Stokes addresses the issue, but indicates that it has not been entirely resolved, as a “raw” numerical approach does not make the grade. Phathinatin!
Actually, understanding none of this, I went to law school.
Women = Money * Time
Time = Money
Women = Money ^ 2
Money is the root of all evil
Women = Evil
1) C = 2πr
2) a0 + a1x + a2x2+ ... + anxn = 0 has at least one complex root for every n > 0. [The Fundamental Theorem of Algebra]
3) f(x) = d/dx ∫ax f(t) dt [with suitable restrictions on f. The Fundamental Theorem of Calculus.]
4) 
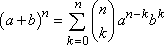
The binomial Theorem.
5) Euler's formula: eiθ = cosθ + i sinθ
All of these are far more important than the Navier-Stokes equation, The Shannon Entropy Information Equation, May's Map, or The Black-Scholes Equation.
Equations changed nothing. What they represented did.
Euclid conceived a point in space, then another and another. Next he moved the points closer together, thereby creating a line. Then he repeated this scenario w/points north to south from the endpoints of his initial line. Lastly, he enclosed his first 3 lines w/a 4th line, giving us a Square; a two dimensional shape! Further he expanded his concept to create a Cube, a three dimensional shape.
The astounding genius of Euclid (as well as the Greeks of Antiquity) created Geometry, the linchpin of Engineering which allowed us to create the structures of the modern world.
... and where’s “e to the pi i = -1” ?
Of course, this is really an encapsulation of “e to the i theta = cos theta + i sin theta”, and this is a pretty big miss IMHO. I don’t think “i squared = -1” covers it.
(((2 * clinton) + 1 obama) - 1/2 harry “blackeye” reid) / the number of dead people who voted for all of them = the stinking stench of the bowels of hell
Yup. Finite element analysis using supercomputers approximate some solutions. But no formal mathematical solution for turbulence has been derived. In fact, that may be an NP-complete problem (in other words not solvable) because of some underlying issues involved.
As a corollary to Euler’s theorem, it fascinates me that:
e^(pi x i) = -1
The fact that three somewhat unrelated concepts such as e, pi and i can be put together to make such an elegant formula blows me away.
I agree. It was a big miss.
It is a remarkable fact
that i to the i
is the same thing
as the square root of one
divided by e to the pi.
That is: ii = √(1/eπ)
This is a remarkable equation, in that 1) a pure imaginary raised to itself is a pure real number 2) the result contains arguably all of the most fundamental constants in mathematics: i, e, π, 1, (and implicitly, 2).
Yes, Navier-Stokes equation would help us understand non-laminar flow. My work involves a dumbed down version of this equation to a simple system of odes with a penalty function on the boundary conditions. I have had no luck in solving these equations, I am going to build a super computer using several raspberry pi computers to try to solve them numerically.
Disclaimer: Opinions posted on Free Republic are those of the individual posters and do not necessarily represent the opinion of Free Republic or its management. All materials posted herein are protected by copyright law and the exemption for fair use of copyrighted works.