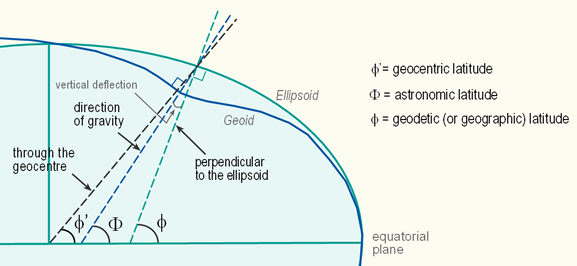
Laplace would be surprised to hear that. That is true on a spherical planet, and on an ellipsoid of rotation, only on the equator and at the poles. It's complicated.
Posted on 04/19/2014 8:40:10 AM PDT by doug from upland
Q: If you could drill a tunnel through the whole planet and then jumped down this tunnel, how would you fall?
Posted on August 3, 2012 by The Physicist
Physicist: This is a beautiful question, in a small part because it’s an interesting thought experiment with some clever math, but mostly because of all the reasons it couldn’t be done and wouldn’t work. Right off the bat; clearly a hole can’t be drilled through the Earth. By the time you’ve gotten no more than 30 miles down (less than 0.4% of the way through) you’ll find your tunnel filling will magma, which tends to gunk up drill bits (also melt everything).
Jumping into a hole drilled through the Earth. What’s the worst that could happen?
But! Assuming that wasn’t an issue, and you’ve got a tube through the Earth (made of unobtainium or something), you still have to contend with the air in the tube. In addition to air-resistance, which on its own would drag you to a stop near the core, just having air in the tube would be really really fatal. The lower you are, the more air is above you, and the higher the pressure. The highest air pressure we see on the surface of the Earth is a little under 16 psi. But keep in mind that we only have about 100 km of real atmosphere above us, and most of that is pretty thin. If the air in the tube were to increase in pressure and temperature the way the atmosphere does, then you’d only have to drop around 50 km before the pressure in the tube was as high as the bottom of the ocean.
Even worse, a big pile of air (like the atmosphere) is hotter at the bottom than at the top (hence all the snow on top of mountains). Temperature varies by about 10°C per km or 30 °F per mile. So, by the time you’ve fallen about 20 miles you’re really on fire a lot. After a few hundred miles (still a long way from the core) you can expect the air to be a ludicrously hot sorta-gas-sorta-fluid, eventually becoming a solid plug.
But! Assuming that there’s no air in the tube, you’re still in trouble. If the Earth is rotating, then in short order you’d be ground against the walls of the tunnel, and would either be pulverized or would slow down and slide to rest near the center of the Earth. This is an effect of “coriolis forces” which show up whenever you try to describe things moving around on spinning things (like planets). To describe it accurately requires the use of angular momentum, but you can picture it pretty well in terms of “higher things move faster”. Because the Earth is turning, how fast you’re moving is proportional to your altitude. Normally this isn’t noticeable. For example, the top of a ten story building is moving about 0.001 mph faster than the ground (ever notice that?), so an object nudged off of the roof can expect to land about 1 millimeter off-target. But over large changes in altitude (and falling through the Earth counts) the effect is very noticeable: about halfway to the center of the Earth you’ll find that you’re moving sideways about 1,500 mph faster than the walls of your tube, which is unhealthy.
The farther from the center you are, the faster you’re moving.
But! Assuming that you’ve got some kind of a super-tube, that the inside of that tube is a vacuum, and that the Earth isn’t turning (and that there’s nothing else to worry about, like building up static electricity or some other unforeseen problem), then you would be free to fall all the way to the far side of the Earth. Once you got there, you would fall right through the Earth again, oscillating back and forth sinusoidally exactly like a bouncing spring or a clock pendulum. It would take you about 42 minutes to make the trip from one side of the Earth to the other.
The clever math behind calculating how an object would fall through the Earth: As you fall all of the layers farther from the center than you cancel out, so you always seem to be falling as though you were on the the surface of a shrinking planet.
What follows is interesting mostly to physics/engineering majors and to almost no one else.
It turns out that spherically symmetric things, which includes things like the Earth, have a cute property: the gravity at any point only depends on the amount of matter below you, and not at all on the amount of matter above you. There are a couple of ways to show this, but since it was done before (with pictures!), take it as read. So, as you fall in all of the layers above you can be ignored (as far as gravity is concerned), and it “feels” as though you’re always falling right next to the surface of a progressively smaller and smaller planet. This, by the way, is just another reason why the exact center of the Earth is in free-fall.
The force of gravity is F = -\frac{GMm}{r^2}, where M is the big mass, and m is the smaller, falling mass. But, since you only have to consider the mass below you, then if the Earth has a fixed density (it doesn’t, but if it did) then you could say M = \rho \frac{4}{3}\pi r^3, where ρ is the density. So, as you’re falling F = -\left(\frac{Gm}{r^2}\right)\left(\rho \frac{4}{3}\pi r^3\right) = -\left(\frac{4}{3}G\rho \pi\right) mr.
Holy crap! This is the (in)famous spring equation, F = – kx! Physicists get very excited when they see this because it’s one of, like, 3 questions that can be exactly answered (seriously). In this case that answer is r(t) = R\cos{\left(t\sqrt{\frac{4}{3}G\rho \pi} \right)}, where R is the radius of the Earth, and t is how long you’ve been falling. Cosine, it’s worth pointing out, is sinusoidal.
Interesting fun-fact: the time it takes to oscillate back-and-forth through a planet is dependent only on the density of that planet and not on the size!
I concur.
That was my thought also.
Kinda like stepping on an elevator on the ground floor and stepping off on the 26th floor.
Robert Hooke is one of the greatest scientific minds ever.
If you are in a free falling elevator would jumping up at the very end, just before impact, save your life?
Laplace would be surprised to hear that. That is true on a spherical planet, and on an ellipsoid of rotation, only on the equator and at the poles. It's complicated.

They can’t get permits to build the keystone pipeline.
He’s assuming there is a vacuum in the hole. You would not reach terminal velocity because there would be no air resistance.
You would accelerate all the way to the center, so you’d get moving pretty fast.
However, acceleration due to gravity would steadily decrease as you approach the center. Your momentum would carry you through the center, then you begin decelerating.
With great enthusiasm, we proceeded to start the hole - in my backyard, because other parents wouldn't let their kids dig in theirs - and after the first afternoon of digging, we actually had a pretty decent sized hole with mounds of dirt and rocks all around.
The next morning, I was woken up to the sounds of my father shouting for me. I came downstairs and my mother grabbed me by the hair and shoved me to the floor in front of my glowering father whose face was rapidly turning a deep shade of red. He simply pointed to the backyard and said "fill it" and walked away.
None of my friends came over to help me fill it. It took pretty much all morning and sure enough, there was not enough dirt to completely fill it and even to this day, some 40 years later, there is still a slight depression in the yard where the aborted hole to China lies unfinished.
http://en.wikipedia.org/wiki/Schuler_tuning
It’s the same period as the period of a satellite orbiting the earth just above the surface.
Someone answering an old qyestion with real science- such a spoil sport - lol
I bet you have more stories to tell... :)
As I understand it, it wouldn’t even need to be directly through the center of the earth. Basically you could drill a straight tunnel (through the curvature of the earth) from LA to NY and get the same effect.
I watch a lot of science shows.
But you don't have to dig to China, just go in the kitchen and open the cabinet doors.
Does that explain why Howard Cosine had such a big nose?
Correct. Maximum velocity would be achieved as the object passes through the center. The maximum rate of acceleration (from x to y) would be realized at the start. The initial acceleration would be 9.8 m/s2. At the earth's center, it would be zero, and at the opposite end of the earth, it would be -9.8 m/s2.
The object would not begin to slow until acceleration goes negative which would occur just after passing through the center point.
Cosines include an angle that’s a-cutie.
I had figured that after digging such a hole, I would end up putting a drain in the Indian Ocean which would result in flooding my entire town. Needless to say, that dissuaded me from putting forth the effort.
Also, down would be come up as you passed the center.
I asked this same question to a physics instructor when I was going to college.
Disclaimer: Opinions posted on Free Republic are those of the individual posters and do not necessarily represent the opinion of Free Republic or its management. All materials posted herein are protected by copyright law and the exemption for fair use of copyrighted works.