Skip to comments.
'Just-in-Case': How to Think About Uncertainty and Global Warming
TCS Daily ^
| 14 Feb 2007
| Arnold Kling
Posted on 02/14/2007 7:33:25 AM PST by jonno
"Let's just say that global warming deniers are now on a par with Holocaust deniers, though one denies the past and the other denies the present and future." -- Ellen Goodman
"Global warming is a false myth and every serious person and scientist says so. It is not fair to refer to the U.N. panel. IPCC is not a scientific institution: it's a political body, a sort of non-government organization of green flavor. It's neither a forum of neutral scientists nor a balanced group of scientists. These people are politicized scientists who arrive there with a one-sided opinion and a one-sided assignment. Also, it's an undignified slapstick that people don't wait for the full report in May 2007 but instead respond, in such a serious way, to the summary for policymakers where all the "but's" are scratched, removed, and replaced by oversimplified theses. This is clearly such an incredible failure of so many people, from journalists to politicians." -- Czech President Vaclav Klaus
Pundits, politicians, and the public have a hard time coming to grips with uncertainty. This makes the atmosphere for debating global warming policy especially foul, because the key issues with global warming are the uncertainties involved. Those who would try to reduce the issue of global warming to a yes-or-no question ("do you believe or do you deny?") are not scientists.
Real scientists understand uncertainty. Real science deals with uncertainty through relentless, skeptical inquiry. Real science resolves arguments not with consensus, but with data.
My understanding of global warming is influenced by my background in applied statistics and economics. There certainly are scientists who have spent more time than I have analyzing the meteorological data. However, before you call me a "hack," make sure that you are capable ...
(Excerpt) Read more at tcsdaily.com ...
TOPICS: Business/Economy; Culture/Society; Government; News/Current Events
KEYWORDS: globalwarming
Navigation: use the links below to view more comments.
first previous 1-20 ... 81-100, 101-120, 121-140, 141-146 next last
To: spunkets
The Plot is tropical, so it's ~equitorial. The dips are due to absorption.
Obviously, the dominant dip at 666 wavenumber is the CO2 15mm line.
The spectrum given in your post is unlabeled. Where did it come from?
The grapic came from a NASA website article:
http://earthobservatory.nasa.gov/Study/Iris/

There are plenty of others all around the internet displaying essentially the same information, this one just overlays CO2 & H20 responses in a way one can see the overlap and saturation of the spectal lines clearly in a single graphic.
"If it weren't saturated it would be a vary narrow dip in the graphic not showing skirt response."
The p, r and q branches are obscured.
Yep, mainly by overlapped water vapor response across the band. The branches would be part of the roughness along the left & right slopes on the primary 15mm line response. The fact the branches are not saturated is what allows the increase in absorption to even be measurable as concentration increases and part of the logaritmic response characteristic rather than the more limiting form such as an exponential like a*(1-e-kC).
It looks like the 5.xxln(C/C,sub>o) is a fitted eq. above a baseline of 278ppmv in 1750. I'll have to look into that.
The analysis comes from Myhre et al. 1998, Geophys.Res.Lett., 25:2715-2718.
From my own integrations of the same spectral data for CO2 the fit is quite good from 100ppmv out beyond 2000ppmv. The numbers I am getting indicate a solid fit with an standard deviation of 0.01 w/m2 throughout that range using a 100meter cell length.
I'm currently building a full integration for an 11km cell length version at mean atmospheric temperature and pressure and CO2 distribution, to see how well the relationship holds for the longer cell length representing a column of the atmosphere and plan on doing a similar analysis for water vapor as well. Figure I just as well take advantage of my access to the software & HITRAN database while I have it.
At present I am working only on the wavenumber region from 555->833 cm-1 (12-18mm wavelength). Given time I'll be expanding the integrations out to cover the wavenumber range from 1 -> 2900 cm-1 corresponding to (3.5-10,000mm).
121
posted on
02/15/2007 9:45:34 PM PST
by
ancient_geezer
(Don't reform it, Replace it.)
To: ancient_geezer; spunkets
I think the two of you have a terminology issue here. When AG says "saturation," S is taking that to mean the CO2 could not absorb more IR and any additional IR would therefore radiate into space. But instead AG is using the term to mean only that all the IR at many wavelengths the Earth *would* radiate currently if there were no atmosphere would be blocked 100% by the atmosphere's CO2.
What is the model for composing the absorption amounts in that chart I wonder? Obviously they can't simply be added because, e.g., at 15µm the CO2 is at 100% and the H2O is at 50% so together they'd be blocking 150% of the radiation which isn't very physical. Seems the right way is f1+f2-f1f2.
To: ancient_geezer
It looks like the 5.xxln(C/C,sub>o) is a fitted eq. above a baseline of 278ppmv in 1750. I'll have to look into that.
what does 1750 data have to do with doing a curve fit against spectral data? You use a database of spectoscopy data to provide the information needed. We are talking about a Line-by-Line analysis of the CO2 & H2O absorption spectrums as a function of concentration and blackbody radiance, a spectroscopic analysis, not a fit to a how concentration varies with time.
123
posted on
02/15/2007 10:00:51 PM PST
by
ancient_geezer
(Don't reform it, Replace it.)
To: edsheppa; spunkets
I think the two of you have a terminology issue here. When AG says "saturation," S is taking that to mean the CO2 could not absorb more IR and any additional IR would therefore radiate into space. But instead AG is using the term to mean only that all the IR at many wavelengths the Earth *would* radiate currently if there were no atmosphere would be blocked 100% by the atmosphere's CO2.
Close, saturation simply means that a spectral line absorbs 100% of the IR available for the temperature involved around the wavelength of the specific absorption line of interest. There are more CO2 molecules than there are photons of IR at the proper wavelengths to be absorbed in a given path length of atmosphere. Increasing concentration effectively broadens the spectral line allowing more absorption by weak lines and the skirts either side of the central spectral line which are not saturated.
What is the model for composing the absorption amounts in that chart I wonder? Obviously they can't simply be added because, e.g., at 15µm the CO2 is at 100% and the H2O is at 50% so together they'd be blocking 150% of the radiation which isn't very physical. Seems the right way is f1+f2-f1f2.
Actually you use the transmission function of CO2 with respect to IR wavelength, and the same for H20 using spectral line data of a specrographic database like HITRAN.
Determine transmission of each component for a specified cell length and concentration for blackbody radiation at the wavelengths of interest and specified temperature, in the particular case say the 288K blackbody emitter for the surface of the earth.
The product of the Transmission values for CO2 & H20 equal the transmission of the IR wavelengths through the cell of the two taken together.
Absorption equals 1-Transmission, multiply the Absorption value by the radiance of the IR wavelengths of interest and you can integrate for the power absorbed by each component separately as well as taken together.
The Transmission spectrum of CO2 & H2O of a standard atmosphere from 10-15 um @ 368ppmv & 736ppmv looks like this example,

spectrum http://www.met.fu-berlin.de/dmg/dmg_home/pics/F_72.gif
which demonstrates how transmission changes for a doubling of CO2 concentration, and the difference between the two as "Residuum" at the bottom. Multiply the residual by the blackbody curve for a particular temperature and integrate you can calculate the IR flux that is absorbed.
124
posted on
02/15/2007 10:37:23 PM PST
by
ancient_geezer
(Don't reform it, Replace it.)
To: ancient_geezer
Actually you use the transmission function... Yeah, that's how I got it. If the absorption fractions are f1 and f2, the transmission fractions are 1-f1 and 1-f2 which you multiply and then apply the inverse map to turn it back into an absorption.
1 - (1-f1)(1-f2) = f1 + f2 - f1f2
The corollary is that there's actually no such thing as 100% absorption but you can get as near as you want.
To: edsheppa
See it now, LOL.
I just look at how I implement it as a simulation on my spreadsheet. I tend to treat the problem as a series of layers or cells feeding light from one to the next in a chain.
Gives me a means to switch components in and out easily for simulating layers of atmosphere with differing characteristics and changing composition.
126
posted on
02/16/2007 12:55:00 AM PST
by
ancient_geezer
(Don't reform it, Replace it.)
To: ancient_geezer; edsheppa
"what does 1750 data have to do with doing a curve fit against spectral data?The eq.
FCO2 = 5.35ln(C/Co) = watts absorbed above the 278ppmv baseline from 1750.
That's my understanding of it. Note that at C=Co, the watts = 0. The eq is an equivalent to Beer's law:
I=Io(1-e- α *c*x) , where α is the absorbtion coefficient, c is the baseline concentration, and x is the pathlength. The eq. is then used to find FCO2 above 1750's value.
FCO2 = Inow - I1750 = I1750(e- α *xc1750 - e- α *xcnow).
Each molecule can absorb at many wavelengths, and each has it's own transition probability. So, the exponential terms are of the form Σn e- αn *xc.
FCO2 = I1750( Σne- αn *xc1750 - Σne- αn *xcnow).
You can see the constants in there. I assume Myhre considered this as a change in intensity due to the probability of more excited states with a change in concentration, dEexcited = A*dc/C. I= A*ln(C/Co), where A represents some sum of absorbtion constants, as above. Fitting obtains, 5.35ln(C/C1750). Then FCO2=I.
At any particular instant, there will be a population of excited molecules. They will decay and reradiate in another direction, they will scatter radiation, and they will decay by transfer of kinetic energy to the surounding gas. The caption to the graph you showed me, then provided a link for says, "The graph at left shows the percentage of energy absorbed in a clear tropical sky by water vapor (green) and carbon dioxide (brown)." In order to absorb 100% of the radiation, there must be unexcited molecules with states available.
"There are more CO2 molecules than there are photons of IR at the proper wavelengths to be absorbed in a given path length of atmosphere.
If that were true, then the caption on that figure could never say 100%. It would have to say something less.
" Increasing concentration effectively broadens the spectral line allowing more absorption by weak lines and the skirts either side of the central spectral line which are not saturated.
Increasing concentration provides more unexcited molecules to absorb radiation. More States are available. The width of those lines around a vibration is due to rotational coupling with the vibration and dopler spreading. The wavelength must match for any particular combo of vibration, rotation and molecular velocity. It is less probable that those vibrations with other angular momentum will be excited. The angular momnetum is coupled, so the vibrational E changes and has max values at J=0 and in the p and r branches, about 4 Δ Js away from there. That's why their peaks are successively lower as the wavelength moves from the base vibrational wavelength. The pressure broadening should be constant.
127
posted on
02/16/2007 1:38:58 PM PST
by
spunkets
("Freedom is about authority", Rudy Giuliani)
To: spunkets; ancient_geezer
Increasing concentration provides more unexcited molecules to absorb radiation.AG's point is that at certain wavelengths there's no more radiation for the gas to absorb, it is being nearly completely blocked by the gas at the current concentration.
A related point is that for those bands already completely blocked, if there were more radiation (e.g. because of warming of the Earth's surface), the current gas concentration could block it so an increase in CO2 concentration isn't meaningful in this way either. This is probably not an important effect because the temperature changes are not that large relative to the absolute temperature.
If that saturation word is bothering you, you might think of it this way instead: the IR radiation is saturated with CO2 and H2O.
To: edsheppa
" the current gas concentration could block it so an increase in CO2 concentration isn't meaningful in this way either. Just to clarify what I focus on. It's really an absorption. If the concentration goes up, say beyond that 1750 number, the energy absorbed goes up, as in 5.35ln(C/Co). If the temp of the Earth's surface goes up, or the Suns output, the the E of the gas at constant concentration goes up, in proportion to the new Io.
"This is probably not an important effect because the temperature changes are not that large relative to the absolute temperature."
LOL! That's whole GW thing. I don't see any significant temp changes, nor E changes that warrant all the doom and gloom in the whole system. The only thing that will change is less than 1% in Energy content at equilibrium in ~2060.
129
posted on
02/16/2007 3:00:15 PM PST
by
spunkets
("Freedom is about authority", Rudy Giuliani)
To: spunkets
FCO2 = 5.35ln(C/Co) = watts absorbed above the 278ppmv baseline from 1750.
That's my understanding of it. Note that at C=Co, the watts = 0.
Actually, Co can be any base you want to apply within the log functions it's effective range, it is not limited to Co=285. It is just as accurate at Co=185ppmv doubling to 390ppmv, as it would be at Co = 500ppmv doubling to 1000ppmv.
It is a general empirical relationship derived from spectroscopic Line by Line integrations.
The eq is an equivalent to Beer's law
Only in a very general sense as Beer's law holds valid for only very low concentrations for a specified monochromatic wavelength where absorption is a linear function of concentrations (e.g. <10ppmv for CO2 in my experience.
refer here for some basics on the applicability of Beer's Law: http://teaching.shu.ac.uk/hwb/chemistry/tutorials/molspec/beers1.htm
A = ebc tells us that absorbance depends on the total quantity of the absorbing compound in the light path through the cuvette. If we plot absorbance against concentration, we get a straight line passing through the origin (0,0).
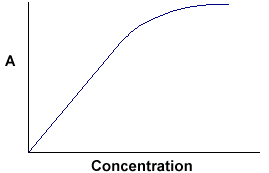 |
Note that the Law is not obeyed at high concentrations. This deviation from the Law is not dealt with here. |
The linear relationship between concentration and absorbance is both simple and straightforward, which is why we prefer to express the Beer-Lambert law using absorbance as a measure of the absorption rather than %T.
At higher concentrations, you approach extinction levels and the relationship breaks down very rapidly.
When you deal in multiple lines at differing strengths and different places in the blackbody radiance curve it becomes nearly a logarithmic function at moderately high concentration and ultimately going to full extinction in the extreme cases of very high concentrations where even weak lines are at extinction levels for the illumination intensities associated with blackbody radiation.
Each molecule can absorb at many wavelengths, and each has it's own transition probability. So, the exponential terms are of the form Sn e- an *xc.
Correct, which would require a Line-by-Line integration with respect to blackbody curve and the multitude of wavelengths involved for high accuracy. Or one may choose to do the Line-By-Line integrations necessary and do a curve fit for the range of concentrations and wavelengths of interest deriving an empirical relationship for general use, which is what the Myhre relation does.
When near extinction levels for the flux levels associated with 200-300K blackbody radiation and multiple lines come into with differing strengths and multiple wavelengths you need a more general approach if you are not going to do Line-by-Line integrations for your calculations for every change in concentration, which can be a computationally expensive approach to modeling. Under such conditions you will find that the overall absorption relation passes through a log response in the 100-2800 ppmv range of concentrations.
An example is the dominant absorption band of 12-18um for CO2:
Given dC is some fraction 320ppmv, i.e. (Concentration-320)/320 for the particular instance
the strong line absorption at its band of wavelengths in the 288K blackbody spectrum fits,
DFw/m2 = 12.6 * (1-e-9.65x10-4*dC)
plotting a strongly limiting function,
While weakline responses elsewhere in the 288K black body spectrum fits
DF w/m2 = 11.9 * (1-e-2.22x10-4*dC)
plotting out as a near linear response up to very high CO2 concentrations
Take the sum of them and you will find that a log relationship can be fit through a significant portion of the curve at concentrations around present day CO2 levels for a representative broad band response, rather than at the limited monochromatic single line response for which Beer's law is generally applied.
Refer to
A Radiative-Convective Model Study of the CO2 Climate Problem
Augustssona & Ramanathan (1977),
Journal of the Atmospheric Sciences, Vol. 34 Issue 3, pp. 448–451 Refer: page 450, Figure 3
For a discussion of how such is applied in a simple model representing climate responses.
Increasing concentration provides more unexcited molecules to absorb radiation. More States are available.
And the effect of that is different from saying:
Increasing concentration effectively broadens the spectral line allowing more absorption by weak lines and the skirts either side of the central spectral line which are not saturated.
how?
The point being that one does not always wish to do full line-by-line integrations for empirical work, especially not when one wants a view of how the whole changes across a range of interest and an empirical relation serves well within known error range. 5% accuracy for an function will do quite well when your other variables are essentially stabs in the dark with estimation errors of 20-100%are the rule as in today's flock of GCMs.
Radiative forcing by well-mixed greenhouse gases:
Estimates from climate models in the
Intergovernmental Panel on Climate Change
(IPCC) Fourth Assessment Report (AR4)
http://www.agu.org/pubs/crossref/2006.../2005JD006713.shtml
http://pubs.giss.nasa.gov/abstracts/2006/Collins_etal.html
http://pubs.giss.nasa.gov/docs/2006/2006_Collins_etal.pdf
Collins, W.D., V. Ramaswamy, M.D. Schwarzkopf, Y. Sun, R.W. Portmann, Q. Fu, S.E.B. Casanova, J.-L. Dufresne, D.W. Fillmore, P.M.D. Forster, V.Y. Galin, L.K. Gohar, W.J. Ingram, D.P. Kratz, M.-P. Lefebvre, J. Li, P. Marquet, V. Oinas, Y. Tsushima, T. Uchiyama, and W.Y. Zhong 2006. Radiative forcing by well-mixed greenhouse gases: Estimates from climate models in the Intergovernmental Panel on Climate Change (IPCC) Fourth Assessment Report (AR4). J. Geophys. Res. 111, D14317, doi:10.1029/2005JD006713.
The radiative effects from increased concentrations of well-mixed greenhouse gases (WMGHGs) represent the most significant and best understood anthropogenic forcing of the climate system. The most comprehensive tools for simulating past and future climates influenced by WMGHGs are fully coupled atmosphere-ocean general circulation models (AOGCMs). Because of the importance of WMGHGs as forcing agents it is essential that AOGCMs compute the radiative forcing by these gases as accurately as possible. We present the results of a radiative transfer model intercomparison between the forcings computed by the radiative parameterizations of AOGCMs and by benchmark line-by-line (LBL) codes. The comparison is focused on forcing by CO2, CH4, N2O, CFC-11, CFC-12, and the increased H2O expected in warmer climates. The models included in the intercomparison include several LBL codes and most of the global models submitted to the Intergovernmental Panel on Climate Change (IPCC) Fourth Assessment Report (AR4). In general, the LBL models are in excellent agreement with each other. However, in many cases, there are substantial discrepancies among the AOGCMs and between the AOGCMs and LBL codes. In some cases this is because the AOGCMs neglect particular absorbers, in particular the near-infrared effects of CH4 and N2O, while in others it is due to the methods for modeling the radiative processes. The biases in the AOGCM forcings are generally largest at the surface level. We quantify these differences and discuss the implications for interpreting variations in forcing and response across the multimodel ensemble of AOGCM simulations assembled for the IPCC AR4.
:
Comparative results of this study show the relative contributions of H2O & CO2 to the anthropogenic global warming hypothesis under IPCC scenarios using the IPCC suite of AOGCMs used in the of their coming AR4 report.
vs the H2O column water vapor increase of 20%.
demonstrating the positive feedback dependency of the models as well as the forcing that each contributes in a relative comparison. Note the more than 20 to 1 forcing of water vapor over CO2 at the surface where global climate change has its most meaningful effect on us poor surface dwelling creatures.
130
posted on
02/16/2007 6:18:52 PM PST
by
ancient_geezer
(Don't reform it, Replace it.)
Comment #131 Removed by Moderator
To: jonno
So lets assume that CO2 causes global warming, how does a carbon tax reduce it? It doesn't. How do alternate fuels reduce CO2, they don't, in fact most increase the total CO2. What does reduce CO2 emissions is using nuclear power for electric generation. Make all new power plants nuclear, and retrofit old power plants as possible. The PBMR technology which is now going into production in South Africa looks real promising. One additional point is nuclear power could be used to generate hydrogen cheaply.
Don't want nuclear, then you don't want to fix the problem you just want the tax money. Quite simple really.
132
posted on
02/16/2007 6:26:58 PM PST
by
Tarpon
To: spunkets
Dang, dropped the graphics on me. Try that last reference with real URL's instead of my harddrive this time:
Radiative forcing by well-mixed greenhouse gases:
Estimates from climate models in the
Intergovernmental Panel on Climate Change
(IPCC) Fourth Assessment Report (AR4)
http://www.agu.org/pubs/crossref/2006.../2005JD006713.shtml
http://pubs.giss.nasa.gov/abstracts/2006/Collins_etal.html
http://pubs.giss.nasa.gov/docs/2006/2006_Collins_etal.pdf
Collins, W.D., V. Ramaswamy, M.D. Schwarzkopf, Y. Sun, R.W. Portmann, Q. Fu, S.E.B. Casanova, J.-L. Dufresne, D.W. Fillmore, P.M.D. Forster, V.Y. Galin, L.K. Gohar, W.J. Ingram, D.P. Kratz, M.-P. Lefebvre, J. Li, P. Marquet, V. Oinas, Y. Tsushima, T. Uchiyama, and W.Y. Zhong 2006. Radiative forcing by well-mixed greenhouse gases: Estimates from climate models in the Intergovernmental Panel on Climate Change (IPCC) Fourth Assessment Report (AR4). J. Geophys. Res. 111, D14317, doi:10.1029/2005JD006713.
The radiative effects from increased concentrations of well-mixed greenhouse gases (WMGHGs) represent the most significant and best understood anthropogenic forcing of the climate system. The most comprehensive tools for simulating past and future climates influenced by WMGHGs are fully coupled atmosphere-ocean general circulation models (AOGCMs). Because of the importance of WMGHGs as forcing agents it is essential that AOGCMs compute the radiative forcing by these gases as accurately as possible. We present the results of a radiative transfer model intercomparison between the forcings computed by the radiative parameterizations of AOGCMs and by benchmark line-by-line (LBL) codes. The comparison is focused on forcing by CO2, CH4, N2O, CFC-11, CFC-12, and the increased H2O expected in warmer climates. The models included in the intercomparison include several LBL codes and most of the global models submitted to the Intergovernmental Panel on Climate Change (IPCC) Fourth Assessment Report (AR4). In general, the LBL models are in excellent agreement with each other. However, in many cases, there are substantial discrepancies among the AOGCMs and between the AOGCMs and LBL codes. In some cases this is because the AOGCMs neglect particular absorbers, in particular the near-infrared effects of CH4 and N2O, while in others it is due to the methods for modeling the radiative processes. The biases in the AOGCM forcings are generally largest at the surface level. We quantify these differences and discuss the implications for interpreting variations in forcing and response across the multimodel ensemble of AOGCM simulations assembled for the IPCC AR4.
:
Comparative results of this study show the relative contributions of H2O & CO2 to the anthropogenic global warming hypothesis under IPCC scenarios using the IPCC suite of AOGCMs used in the of their coming AR4 report.

vs the H2O column water vapor increase of 20%.

demonstrating the positive feedback dependancy of the models as well as the forcing that each contributes in a relative comparison. Note the more than 20 to 1 forcing of water vapor over CO2 at the surface where global climate change has its most meaningful effect on us poor surface dwelling creatures.
133
posted on
02/16/2007 6:30:06 PM PST
by
ancient_geezer
(Don't reform it, Replace it.)
To: spunkets
LOL! That's whole GW thing. I don't see any significant temp changes, nor E changes that warrant all the doom and gloom in the whole system. The only thing that will change is less than 1% in Energy content at equilibrium in ~2060.
I certainly don't dissagree there, that's obvious to anyone who takes the time and effort to look into what the the real relationships are and note the whole AGW argument relies on hypotheticals that simply don't pan out when applied to the real world where the infinitesmal absorptions of CO2 is set against solar activity related effects on the atmosphere, changing water vapor content, clouds, ...
134
posted on
02/16/2007 6:39:36 PM PST
by
ancient_geezer
(Don't reform it, Replace it.)
To: spunkets; edsheppa
Dang, try one more time, maybe get it right this time and go to bed where this decrepit ole man belongs.
Radiative forcing by well-mixed greenhouse gases:
Estimates from climate models in the
Intergovernmental Panel on Climate Change
(IPCC) Fourth Assessment Report (AR4)
http://www.agu.org/pubs/crossref/2006.../2005JD006713.shtml
http://pubs.giss.nasa.gov/abstracts/2006/Collins_etal.html
http://pubs.giss.nasa.gov/docs/2006/2006_Collins_etal.pdf
Collins, W.D., V. Ramaswamy, M.D. Schwarzkopf, Y. Sun, R.W. Portmann, Q. Fu, S.E.B. Casanova, J.-L. Dufresne, D.W. Fillmore, P.M.D. Forster, V.Y. Galin, L.K. Gohar, W.J. Ingram, D.P. Kratz, M.-P. Lefebvre, J. Li, P. Marquet, V. Oinas, Y. Tsushima, T. Uchiyama, and W.Y. Zhong 2006. Radiative forcing by well-mixed greenhouse gases: Estimates from climate models in the Intergovernmental Panel on Climate Change (IPCC) Fourth Assessment Report (AR4). J. Geophys. Res. 111, D14317, doi:10.1029/2005JD006713.
The radiative effects from increased concentrations of well-mixed greenhouse gases (WMGHGs) represent the most significant and best understood anthropogenic forcing of the climate system. The most comprehensive tools for simulating past and future climates influenced by WMGHGs are fully coupled atmosphere-ocean general circulation models (AOGCMs). Because of the importance of WMGHGs as forcing agents it is essential that AOGCMs compute the radiative forcing by these gases as accurately as possible. We present the results of a radiative transfer model intercomparison between the forcings computed by the radiative parameterizations of AOGCMs and by benchmark line-by-line (LBL) codes. The comparison is focused on forcing by CO2, CH4, N2O, CFC-11, CFC-12, and the increased H2O expected in warmer climates. The models included in the intercomparison include several LBL codes and most of the global models submitted to the Intergovernmental Panel on Climate Change (IPCC) Fourth Assessment Report (AR4). In general, the LBL models are in excellent agreement with each other. However, in many cases, there are substantial discrepancies among the AOGCMs and between the AOGCMs and LBL codes. In some cases this is because the AOGCMs neglect particular absorbers, in particular the near-infrared effects of CH4 and N2O, while in others it is due to the methods for modeling the radiative processes. The biases in the AOGCM forcings are generally largest at the surface level. We quantify these differences and discuss the implications for interpreting variations in forcing and response across the multimodel ensemble of AOGCM simulations assembled for the IPCC AR4.
:
Comparative results of this study show the relative contributions of H2O & CO2 to the anthropogenic global warming hypothesis under IPCC scenarios using the IPCC suite of AOGCMs used in the of their coming AR4 report.

vs the H2O column water vapor increase of 20%.

demonstrating the positive feedback dependancy of the models as well as the forcing that each contributes in a relative comparison. Note the more than 20 to 1 forcing of water vapor over CO2 at the surface where global climate change has its most meaningful effect on us poor surface dwelling creatures.
There that's better.
Looking at those graphics again, one can't but help wonder how settled can climate science be when the AGW modelers apparently can't even agree among themselves what can happen with even a simple step change of single inputs in isolation.
135
posted on
02/16/2007 6:56:48 PM PST
by
ancient_geezer
(Don't reform it, Replace it.)
To: ancient_geezer
" Actually, Co can be any base you want to apply within the log functions it's effective range, it is not limited to Co=285. It is just as accurate at Co=185ppmv doubling to 390ppmv, as it would be at Co = 500ppmv doubling to 1000ppmv. It is a general empirical relationship derived from spectroscopic Line by Line integrations. It comes from the solution of the diff eq,
dEexcited = A*dc/C.
I= A*ln(C) -ln(Co) + const
The constant is zero, and the absorbed watts is above what's absorbed at Co. A is evaluated as a sum of the absorption coefficients, the path length, and contains a base Io. It's ng if any of those change, or the validity of the sum of the absorption coeffs is violated.
"Only in a very general sense as Beer's law holds valid for only very low concentrations for a specified monochromatic wavelength where absorption is a linear function of concentrations (e.g. <10ppmv for CO2 in my experience."
Only, because only one absorption coefficient is considered. I gave the general form, which is generally valid anytime. The gen diff eq is,
dI/I = Σn αncx dc(or dx, depending)
Re: Increasing concentration provides more unexcited molecules to absorb radiation. More States are available.
" And the effect of that is different from saying:
Increasing concentration effectively broadens the spectral line allowing more absorption by weak lines and the skirts either side of the central spectral line which are not saturated.
how?"
Broadening of spectral lines is a real effect caused by pressure, Doppler effects, and temperature. Increasing the concentration just adds to the number of States available. The lower concentration had the same lines being filled. It's an equipartition of energy thing. A higher concentration just allows that much more energy into the same modes. The modes fill according to the probability of transition for that mode. That probability is quantified in the absorption coefficients. No mode is ever saturated in these cases. Their absorption coefficients are constants, and the probability of exciting a mode stays the same. There's a Boltzmann dist of excited States at any temp. Only certain transitions are allowed. So the effective concentration is always lower. That doesn't mean the strong peaks are "saturated". It's means the molecules are in another State, that doesn't allow a transition.
THanks for the links. I see GW as not amounting to anything significant, until after the condition of 2060 is reached, where the total E is still less than 1% greater than the good old days of watermelon delight. Any system will move to minimize the E in any path between equilibrium conditions. It's the endpoints that are important. There's nothing significantly different in the endpoints, nor is there any reason for wild occurrences to appear, that would not have appeared before the perturbation.
136
posted on
02/16/2007 8:30:04 PM PST
by
spunkets
("Freedom is about authority", Rudy Giuliani)
To: spunkets
Re: Increasing concentration provides more unexcited molecules to absorb radiation. More States are available. No mode is ever saturated in these cases.
Of little relavance when flux is already being absorbed near extinction levels at high concentrations. When there is little more to be absorbed a linear increment in the number of molecules involved has less effect as concentration increases.
All increasing concentration can do is ultimately approach an asymtotic boundry set by the free flux left to be absorbed however marginal that might be.
The net effect at high concentrations is essentially absorption approaching a logarithmic relationship to concentration at modrately high concentrations, clearly at a declining rate as compared to the near linear increase in absorption with change in concentration that occurs at low concentrations.
137
posted on
02/16/2007 11:06:19 PM PST
by
ancient_geezer
(Don't reform it, Replace it.)
To: ancient_geezer
"The net effect at high concentrations is essentially absorption approaching a logarithmic relationship to concentration at modrately high concentrations, clearly at a declining rate as compared to the near linear increase in absorption with change in concentration that occurs at low concentrations." absorbance = (1- Σne-αn*C)
The relation is never linear, even when all αns are considered. It's only approximately linear over some range. The ~ log linear absorbance holds for any decade, regardless of concentration.
138
posted on
02/17/2007 7:08:29 AM PST
by
spunkets
("Freedom is about authority", Rudy Giuliani)
To: ancient_geezer
The eq I = A ln(C/Co) Represents an increase in absorbance over some fixed concentration Co. The factor A, must be evaluated at some fixed Po and Co. If either of those change, the relation no longer holds.
139
posted on
02/17/2007 7:40:47 AM PST
by
spunkets
("Freedom is about authority", Rudy Giuliani)
To: spunkets
Guess these folk just lie then.
Do you even begin to understand the difference between practical approximation, and last decimal analysis? And why one might prefer to use an accurate approximation to express a relationship over a theoretical relationship with a precision beyond that which is necessary for practical utilization?
http://teaching.shu.ac.uk/hwb/chemistry/tutorials/molspec/beers1.htm
A = ebc tells us that absorbance depends on the total quantity of the absorbing compound in the light path through the cuvette. If we plot absorbance against concentration, we get a straight line passing through the origin (0,0).
 |
Note that the Law is not obeyed at high concentrations. This deviation from the Law is not dealt with here. |
The linear relationship between concentration and absorbance is both simple and straightforward, which is why we prefer to express the Beer-Lambert law using absorbance as a measure of the absorption rather than %T.
You tire me with your argument to the last decimal point. Approximation is a useful tool for building practical measures and expressing the effects of a change in practical conditions.
The issue is one of fairly expressing a relationship in terms that are useful and practical, not to the last theoretical decimal place to the point of losing sight of that which one needs to convey.
I didn't say it was ever "linear" overall, nor have I even said it is ever completely "logrithmic" overall.
What I have said it that in different parts of the response curve, the relationship approaches linear or logrithmic as to make no difference for practical purposes in estimating the amount of forcing to derived from a change in that concentration.
At concentrations of CO2 that have actually existed in the atmosphere, the response is so near logrithmic as to be a useful assumption for approximation over a wide range of values.
On the other hand for a gas like Freon, at extremely low concentrations, a linear approximation suffices for the range of concentations one would resonable expect to exist. For a gas in mid ranges of concentration like methane, one may use a square root function to represent the the absorption of radiative flux.
Obaining a simpler and useful approximation for existing conditions is what fitting an empirical function is all about.
The use of formulas' like DF = 5.35 ln(C/C0) wm-2 [Myhre et al. 1998, Geophys.Res.Lett., 25:2715-2718], provides a useful tool for expressing how a system responds within a practical and expected range of change as opposed to the full last decimal analysis that conveys little practical understanding for reason of its complexity.
Hence we see the prevalent use of approximations instead of volumes of equations that ultimately cause the eyes to gloss over and the point one attempts of convey lost by audience.
http://www.cmdl.noaa.gov/aggi/#table1
RADIATIVE FORCING CALCULATIONS
To determine the total radiative forcing of the greenhouse gases, we have used IPCC (2001) recommended expressions to convert greenhouse gas changes, relative to 1750, to instantaneous radiative forcing (see Table 1). This is not a measure of the integrated climate forcing which can only be determined through an atmospheric radiative transfer model. In addition, only the direct forcing has been calculated. Model-dependent feedbacks, for example, due to water vapor and ozone depletion, other short-lived gases and aerosols have not been included. Contrary to climate models, these results are thus based mainly on measurements and have relatively high precision.
Table 1. Expressions for Calculating Radiative Forcing*
| Trace Gas |
Simplified Expression
Radiative Forcing, ?F (Wm-2) |
Constant |
| CO2 |
?F = aln(C/Co) |
a = 5.35 |
| CH4 |
?F = ß(M½ - Mo½) - [f(M,No) - f(Mo,No)] |
ß = 0.036 |
| N2O |
?F = e(N½ - No½) - [f(Mo,N) - f(Mo,No)] |
e = 0.12 |
| CFC-11 |
?F = ?(X - Xo) |
? = 0.25 |
| CFC-12 |
?F = ?(X - Xo) |
? = 0.32 |
| *IPCC (2001) The subscript "o" denotes the unperturbed (1750) concentration f(M,N) = 0.47ln[1 + 2.01x10-5 (MN)0.75 + 5.31x10-15M(MN)1.52]
C is CO2 in ppm, M is CH4 in ppb
N is N2O in ppb, X is CFC in ppb
Co = 278 ppm, Mo = 700 ppb, No = 270 ppb, Xo = 0
|
140
posted on
02/17/2007 8:24:55 AM PST
by
ancient_geezer
(Don't reform it, Replace it.)
Navigation: use the links below to view more comments.
first previous 1-20 ... 81-100, 101-120, 121-140, 141-146 next last
Disclaimer:
Opinions posted on Free Republic are those of the individual
posters and do not necessarily represent the opinion of Free Republic or its
management. All materials posted herein are protected by copyright law and the
exemption for fair use of copyrighted works.
FreeRepublic.com is powered by software copyright 2000-2008 John Robinson




