[spunkets]

"The net effect at high concentrations is essentially absorption approaching a logarithmic relationship to concentration at modrately high concentrations, clearly at a declining rate as compared to the near linear increase in absorption with change in concentration that occurs at low concentrations."

absorbance = (1- Σ_ne^-α_n*C)

The relation is never linear, even when all α_ns are considered. It's only approximately linear over some range. The ~ log linear absorbance holds for any decade, regardless of concentration.

[spunkets]

The eq I = A ln(C/C_o) Represents an increase in absorbance over some fixed concentration C_o. The factor A, must be evaluated at some fixed P_o and C_o. If either of those change, the relation no longer holds.

[ancient_geezer]

Guess these folk just lie then.

Do you even begin to understand the difference between practical approximation, and last decimal analysis? And why one might prefer to use an accurate approximation to express a relationship over a theoretical relationship with a precision beyond that which is necessary for practical utilization?

http://teaching.shu.ac.uk/hwb/chemistry/tutorials/molspec/beers1.htm

 

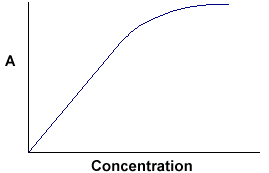
A = ebc tells us that absorbance depends on the total quantity of the absorbing compound in the light path through the cuvette. If we plot absorbance against concentration, we get a straight line passing through the origin (0,0).

Note that the Law is not obeyed at high concentrations. This deviation from the Law is not dealt with here.

The linear relationship between concentration and absorbance is both simple and straightforward, which is why we prefer to express the Beer-Lambert law using absorbance as a measure of the absorption rather than %T.

 

You tire me with your argument to the last decimal point. Approximation is a useful tool for building practical measures and expressing the effects of a change in practical conditions.

The issue is one of fairly expressing a relationship in terms that are useful and practical, not to the last theoretical decimal place to the point of losing sight of that which one needs to convey.

I didn't say it was ever "linear" overall, nor have I even said it is ever completely "logrithmic" overall.

What I have said it that in different parts of the response curve, the relationship approaches linear or logrithmic as to make no difference for practical purposes in estimating the amount of forcing to derived from a change in that concentration.

At concentrations of CO2 that have actually existed in the atmosphere, the response is so near logrithmic as to be a useful assumption for approximation over a wide range of values.

On the other hand for a gas like Freon, at extremely low concentrations, a linear approximation suffices for the range of concentations one would resonable expect to exist. For a gas in mid ranges of concentration like methane, one may use a square root function to represent the the absorption of radiative flux.

Obaining a simpler and useful approximation for existing conditions is what fitting an empirical function is all about.

The use of formulas' like DF = 5.35 ln(C/C₀) wm^-2 [Myhre et al. 1998, Geophys.Res.Lett., 25:2715-2718], provides a useful tool for expressing how a system responds within a practical and expected range of change as opposed to the full last decimal analysis that conveys little practical understanding for reason of its complexity.

Hence we see the prevalent use of approximations instead of volumes of equations that ultimately cause the eyes to gloss over and the point one attempts of convey lost by audience.

 

http://www.cmdl.noaa.gov/aggi/#table1

RADIATIVE FORCING CALCULATIONS
 
To determine the total radiative forcing of the greenhouse gases, we have used IPCC (2001) recommended expressions to convert greenhouse gas changes, relative to 1750, to instantaneous radiative forcing (see Table 1).  This is not a measure of the integrated climate forcing which can only be determined through an atmospheric radiative transfer model.  In addition, only the direct forcing has been calculated.  Model-dependent feedbacks, for example, due to water vapor and ozone depletion, other short-lived gases and aerosols have not been included.  Contrary to climate models, these results are thus based mainly on measurements and have relatively high precision.

Table 1. Expressions for Calculating Radiative Forcing*

 

Trace Gas	Simplified Expression Radiative Forcing, ?F (Wm-2)	Constant
CO2	?F = aln(C/Co)	a = 5.35
CH4	?F = ß(M½ - Mo½) - [f(M,No) - f(Mo,No)]	ß = 0.036
N2O	?F = e(N½ - No½) - [f(Mo,N) - f(Mo,No)]	e = 0.12
CFC-11	?F = ?(X - Xo)	? = 0.25
CFC-12	?F = ?(X - Xo)	? = 0.32
*IPCC (2001) The subscript "o" denotes the unperturbed (1750) concentration f(M,N) = 0.47ln[1 + 2.01x10-5 (MN)0.75 + 5.31x10-15M(MN)1.52] C is CO2 in ppm, M is CH4 in ppb N is N2O in ppb, X is CFC in ppb Co = 278 ppm, Mo = 700 ppb, No = 270 ppb, Xo = 0