Math question?

[Louis Foxwell]

1 in 6. Odds do not change based on number of times. The odds are the same for every roll of the dice.

[American in Israel]

Well for the dice, its exactly the same, prior rolls do not influence latter rolls.

[Paladin2]

multiplication. potentially factorials.

[gorush]

80% chance, I believe.

[Gamecock]

Exactly.

[Fester Chugabrew]

I’m no math whiz either, but I think in the case of dice it would be expressed in a percentage as 100/6 = 16.6667%

[Jewbacca]

How about:

(number of times you roll the dice) * (1/6)

of course, this proves statistians are liars, in that you could theoretically roll it 6 times and never get the number you were looking for.

(There’s actually a real way to do this, but I don’t have any coffee in me.)

[IMR 4350]

What’s the event?

Is it a human influenced event?

[alexander_busek]

What are the chances I will get a "five" if I roll the dice six times?

Your wording is a little unclear. If you mean "What are the chances that I will get a 'five' six times in a row?", that that would be one thirty-sixth.

Regards,

[gorush]

(83%, actually)

[Jewbacca]

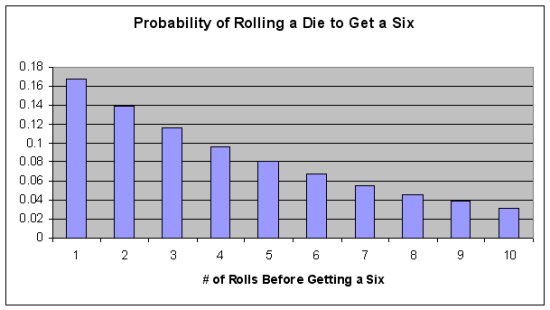
Sorry, the real way to do this is to note you have a 5/6 chance of not hitting your number each roll.

[JPG]

Interesting factoid. My brother was once at a crap table and observed 5 hard 10's rolled in a row.

That 'can't' happen....but it did.

[pelican001]

Just calculate the chance of NOT getting a 5 in 6 roles of the dice:

5/6 * 5/6 * 5/6 * 5/6 * 5/6 * 5/6 = 0.335

So the chance of getting at least one 5 is 1 - 0.335 = .665

or 66.5%

[MNDude]

OK, basically I’m trying to put together a call center to reach out to our clients. I know that there’s a 16% chance someone will connect with someone while making a phone call.

So I’m trying to calculate how many people we will reach if we make calls out to 1000 people, and we call each one up to six times. (stop calling those once we’ve made contact of course).

[So Cal Rocket]

Just calculate the chance of NOT getting a 5 in 6 roles of the dice:

5/6 * 5/6 * 5/6 * 5/6 * 5/6 * 5/6 = 0.335

So the chance of getting at least one 5 is 1 - 0.335 = .665

or 66.5%

---

This is the correct answer.

[Leaning Right]

What are the chances I will get a "five" if I roll the dice six times?

Think of it this way. What's the chance of rolling one die one time and NOT getting a 5? It's 5/6.

So the chances of rolling a die six times and not getting a 5 is: (5/6) to the power of 6. That's 0.335. Then subtract that from 1 (100%). Result: 0.665 or 66.5%.

Disclaimer: I did this on a untrustworthy calculator. Please do not use my result to build a rocket or anything like that.

[Jewbacca]

Like this for the 36 rolls:

The “36” is in superscript (ie to the 36th power)

1-(5/6)36 = 99.86%

[bkepley]

Just calculate the chance of NOT getting a 5 in 6 roles of the dice:

5/6 * 5/6 * 5/6 * 5/6 * 5/6 * 5/6 = 0.335

So the chance of getting at least one 5 is 1 - 0.335 = .665

or 66.5%

Excellent!

[Jewbacca]

1- (.84) 1000 = answer

The 1000 is in superscript.