 reationists occasionally charge that evolution is useless as a scientific theory because it produces no practical benefits and has no relevance to daily life. However, the evidence of biology alone shows that this claim is untrue. There are numerous natural phenomena for which evolution gives us a sound theoretical underpinning. To name just one, the observed development of resistance - to insecticides in crop pests, to antibiotics in bacteria, to chemotherapy in cancer cells, and to anti-retroviral drugs in viruses such as HIV - is a straightforward consequence of the laws of mutation and selection, and understanding these principles has helped us to craft strategies for dealing with these harmful organisms. The evolutionary postulate of common descent has aided the development of new medical drugs and techniques by giving researchers a good idea of which organisms they should experiment on to obtain results that are most likely to be relevant to humans. Finally, the principle of selective breeding has been used to great effect by humans to create customized organisms unlike anything found in nature for their own benefit. The canonical example, of course, is the many varieties of domesticated dogs (breeds as diverse as bulldogs, chihuahuas and dachshunds have been produced from wolves in only a few thousand years), but less well-known examples include cultivated maize (very different from its wild relatives, none of which have the familiar "ears" of human-grown corn), goldfish (like dogs, we have bred varieties that look dramatically different from the wild type), and dairy cows (with immense udders far larger than would be required just for nourishing offspring).
reationists occasionally charge that evolution is useless as a scientific theory because it produces no practical benefits and has no relevance to daily life. However, the evidence of biology alone shows that this claim is untrue. There are numerous natural phenomena for which evolution gives us a sound theoretical underpinning. To name just one, the observed development of resistance - to insecticides in crop pests, to antibiotics in bacteria, to chemotherapy in cancer cells, and to anti-retroviral drugs in viruses such as HIV - is a straightforward consequence of the laws of mutation and selection, and understanding these principles has helped us to craft strategies for dealing with these harmful organisms. The evolutionary postulate of common descent has aided the development of new medical drugs and techniques by giving researchers a good idea of which organisms they should experiment on to obtain results that are most likely to be relevant to humans. Finally, the principle of selective breeding has been used to great effect by humans to create customized organisms unlike anything found in nature for their own benefit. The canonical example, of course, is the many varieties of domesticated dogs (breeds as diverse as bulldogs, chihuahuas and dachshunds have been produced from wolves in only a few thousand years), but less well-known examples include cultivated maize (very different from its wild relatives, none of which have the familiar "ears" of human-grown corn), goldfish (like dogs, we have bred varieties that look dramatically different from the wild type), and dairy cows (with immense udders far larger than would be required just for nourishing offspring).
Critics might charge that creationists can explain these things without recourse to evolution. For example, creationists often explain the development of resistance to antibiotic agents in bacteria, or the changes wrought in domesticated animals by artificial selection, by presuming that God decided to create organisms in fixed groups, called "kinds" or baramin. Though natural microevolution or human-guided artificial selection can bring about different varieties within the originally created "dog-kind," or "cow-kind," or "bacteria-kind" (!), no amount of time or genetic change can transform one "kind" into another. However, exactly how the creationists determine what a "kind" is, or what mechanism prevents living things from evolving beyond its boundaries, is invariably never explained.
But in the last few decades, the continuing advance of modern technology has brought about something new. Evolution is now producing practical benefits in a very different field, and this time, the creationists cannot claim that their explanation fits the facts just as well. This field is computer science, and the benefits come from a programming strategy called genetic algorithms. This essay will explain what genetic algorithms are and will show how they are relevant to the evolution/creationism debate.
What is a genetic algorithm?
|
|
Concisely stated, a genetic algorithm (or GA for short) is a programming technique that mimics biological evolution as a problem-solving strategy. Given a specific problem to solve, the input to the GA is a set of potential solutions to that problem, encoded in some fashion, and a metric called a fitness function that allows each candidate to be quantitatively evaluated. These candidates may be solutions already known to work, with the aim of the GA being to improve them, but more often they are generated at random.
The GA then evaluates each candidate according to the fitness function. In a pool of randomly generated candidates, of course, most will not work at all, and these will be deleted. However, purely by chance, a few may hold promise - they may show activity, even if only weak and imperfect activity, toward solving the problem.
These promising candidates are kept and allowed to reproduce. Multiple copies are made of them, but the copies are not perfect; random changes are introduced during the copying process. These digital offspring then go on to the next generation, forming a new pool of candidate solutions, and are subjected to a second round of fitness evaluation. Those candidate solutions which were worsened, or made no better, by the changes to their code are again deleted; but again, purely by chance, the random variations introduced into the population may have improved some individuals, making them into better, more complete or more efficient solutions to the problem at hand. Again these winning individuals are selected and copied over into the next generation with random changes, and the process repeats. The expectation is that the average fitness of the population will increase each round, and so by repeating this process for hundreds or thousands of rounds, very good solutions to the problem can be discovered.
As astonishing and counterintuitive as it may seem to some, genetic algorithms have proven to be an enormously powerful and successful problem-solving strategy, dramatically demonstrating the power of evolutionary principles. Genetic algorithms have been used in a wide variety of fields to evolve solutions to problems as difficult as or more difficult than those faced by human designers. Moreover, the solutions they come up with are often more efficient, more elegant, or more complex than anything comparable a human engineer would produce. In some cases, genetic algorithms have come up with solutions that baffle the programmers who wrote the algorithms in the first place!
Methods of representation
Before a genetic algorithm can be put to work on any problem, a method is needed to encode potential solutions to that problem in a form that a computer can process. One common approach is to encode solutions as binary strings: sequences of 1's and 0's, where the digit at each position represents the value of some aspect of the solution. Another, similar approach is to encode solutions as arrays of integers or decimal numbers, with each position again representing some particular aspect of the solution. This approach allows for greater precision and complexity than the comparatively restricted method of using binary numbers only and often "is intuitively closer to the problem space" (Fleming and Purshouse 2002, p. 1228).
This technique was used, for example, in the work of Steffen Schulze-Kremer, who wrote a genetic algorithm to predict the three-dimensional structure of a protein based on the sequence of amino acids that go into it (Mitchell 1996, p. 62). Schulze-Kremer's GA used real-valued numbers to represent the so-called "torsion angles" between the peptide bonds that connect amino acids. (A protein is made up of a sequence of basic building blocks called amino acids, which are joined together like the links in a chain. Once all the amino acids are linked, the protein folds up into a complex three-dimensional shape based on which amino acids attract each other and which ones repel each other. The shape of a protein determines its function.) Genetic algorithms for training neural networks often use this method of encoding also.
A third approach is to represent individuals in a GA as strings of letters, where each letter again stands for a specific aspect of the solution. One example of this technique is Hiroaki Kitano's "grammatical encoding" approach, where a GA was put to the task of evolving a simple set of rules called a context-free grammar that was in turn used to generate neural networks for a variety of problems (Mitchell 1996, p. 74).
The virtue of all three of these methods is that they make it easy to define operators that cause the random changes in the selected candidates: flip a 0 to a 1 or vice versa, add or subtract from the value of a number by a randomly chosen amount, or change one letter to another. (See the section on Methods of change for more detail about the genetic operators.) Another strategy, developed principally by John Koza of Stanford University and called genetic programming, represents programs as branching data structures called trees (Koza et al. 2003, p. 35). In this approach, random changes can be brought about by changing the operator or altering the value at a given node in the tree, or replacing one subtree with another.
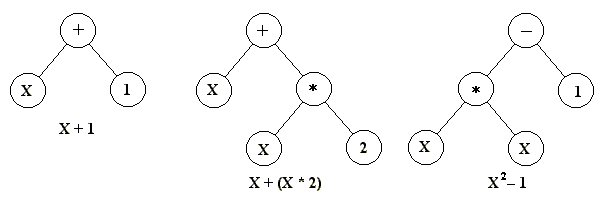
Figure 1: Three simple program trees of the kind normally used in genetic programming. The mathematical expression that each one represents is given underneath.
It is important to note that evolutionary algorithms do not need to represent candidate solutions as data strings of fixed length. Some do represent them in this way, but others do not; for example, Kitano's grammatical encoding discussed above can be efficiently scaled to create large and complex neural networks, and Koza's genetic programming trees can grow arbitrarily large as necessary to solve whatever problem they are applied to.
Methods of selection
There are many different techniques which a genetic algorithm can use to select the individuals to be copied over into the next generation, but listed below are some of the most common methods. Some of these methods are mutually exclusive, but others can be and often are used in combination.
Elitist selection: The most fit members of each generation are guaranteed to be selected. (Most GAs do not use pure elitism, but instead use a modified form where the single best, or a few of the best, individuals from each generation are copied into the next generation just in case nothing better turns up.)
Fitness-proportionate selection: More fit individuals are more likely, but not certain, to be selected.
Roulette-wheel selection: A form of fitness-proportionate selection in which the chance of an individual's being selected is proportional to the amount by which its fitness is greater or less than its competitors' fitness. (Conceptually, this can be represented as a game of roulette - each individual gets a slice of the wheel, but more fit ones get larger slices than less fit ones. The wheel is then spun, and whichever individual "owns" the section on which it lands each time is chosen.)
Scaling selection: As the average fitness of the population increases, the strength of the selective pressure also increases and the fitness function becomes more discriminating. This method can be helpful in making the best selection later on when all individuals have relatively high fitness and only small differences in fitness distinguish one from another.
Tournament selection: Subgroups of individuals are chosen from the larger population, and members of each subgroup compete against each other. Only one individual from each subgroup is chosen to reproduce.
Rank selection: Each individual in the population is assigned a numerical rank based on fitness, and selection is based on this ranking rather than absolute differences in fitness. The advantage of this method is that it can prevent very fit individuals from gaining dominance early at the expense of less fit ones, which would reduce the population's genetic diversity and might hinder attempts to find an acceptable solution.
Generational selection: The offspring of the individuals selected from each generation become the entire next generation. No individuals are retained between generations.
Steady-state selection: The offspring of the individuals selected from each generation go back into the pre-existing gene pool, replacing some of the less fit members of the previous generation. Some individuals are retained between generations.
Hierarchical selection: Individuals go through multiple rounds of selection each generation. Lower-level evaluations are faster and less discriminating, while those that survive to higher levels are evaluated more rigorously. The advantage of this method is that it reduces overall computation time by using faster, less selective evaluation to weed out the majority of individuals that show little or no promise, and only subjecting those who survive this initial test to more rigorous and more computationally expensive fitness evaluation.
Methods of change
Once selection has chosen fit individuals, they must be randomly altered in hopes of improving their fitness for the next generation. There are two basic strategies to accomplish this. The first and simplest is called mutation. Just as mutation in living things changes one gene to another, so mutation in a genetic algorithm causes small alterations at single points in an individual's code.
The second method is called crossover, and entails choosing two individuals to swap segments of their code, producing artificial "offspring" that are combinations of their parents. This process is intended to simulate the analogous process of recombination that occurs to chromosomes during sexual reproduction. Common forms of crossover include single-point crossover, in which a point of exchange is set at a random location in the two individuals' genomes, and one individual contributes all its code from before that point and the other contributes all its code from after that point to produce an offspring, and uniform crossover, in which the value at any given location in the offspring's genome is either the value of one parent's genome at that location or the value of the other parent's genome at that location, chosen with 50/50 probability.
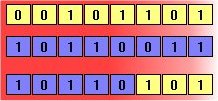

Figure 2: Crossover and mutation. The above diagrams illustrate the effect of each of these genetic operators on individuals in a population of 8-bit strings. The upper diagram shows two individuals undergoing single-point crossover; the point of exchange is set between the fifth and sixth positions in the genome, producing a new individual that is a hybrid of its progenitors. The second diagram shows an individual undergoing mutation at position 4, changing the 0 at that position in its genome to a 1.
Other problem-solving techniques
With the rise of artificial life computing and the development of heuristic methods, other computerized problem-solving techniques have emerged that are in some ways similar to genetic algorithms. This section explains some of these techniques, in what ways they resemble GAs and in what ways they differ.
- Neural networks
A neural network, or neural net for short, is a problem-solving method based on a computer model of how neurons are connected in the brain. A neural network consists of layers of processing units called nodes joined by directional links: one input layer, one output layer, and zero or more hidden layers in between. An initial pattern of input is presented to the input layer of the neural network, and nodes that are stimulated then transmit a signal to the nodes of the next layer to which they are connected. If the sum of all the inputs entering one of these virtual neurons is higher than that neuron's so-called activation threshold, that neuron itself activates, and passes on its own signal to neurons in the next layer. The pattern of activation therefore spreads forward until it reaches the output layer and is there returned as a solution to the presented input. Just as in the nervous system of biological organisms, neural networks learn and fine-tune their performance over time via repeated rounds of adjusting their thresholds until the actual output matches the desired output for any given input. This process can be supervised by a human experimenter or may run automatically using a learning algorithm (Mitchell 1996, p. 52). Genetic algorithms have been used both to build and to train neural networks.
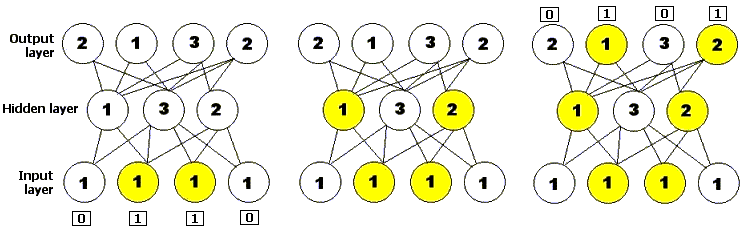
Figure 3: A simple feedforward neural network, with one input layer consisting of four neurons, one hidden layer consisting of three neurons, and one output layer consisting of four neurons. The number on each neuron represents its activation threshold: it will only fire if it receives at least that many inputs. The diagram shows the neural network being presented with an input string and shows how activation spreads forward through the network to produce an output.
- Hill-climbing
Similar to genetic algorithms, though more systematic and less random, a hill-climbing algorithm begins with one initial solution to the problem at hand, usually chosen at random. The string is then mutated, and if the mutation results in higher fitness for the new solution than for the previous one, the new solution is kept; otherwise, the current solution is retained. The algorithm is then repeated until no mutation can be found that causes an increase in the current solution's fitness, and this solution is returned as the result (Koza et al. 2003, p. 59). (To understand where the name of this technique comes from, imagine that the space of all possible solutions to a given problem is represented as a three-dimensional contour landscape. A given set of coordinates on that landscape represents one particular solution. Those solutions that are better are higher in altitude, forming hills and peaks; those that are worse are lower in altitude, forming valleys. A "hill-climber" is then an algorithm that starts out at a given point on the landscape and moves inexorably uphill.) Hill-climbing is what is known as a greedy algorithm, meaning it always makes the best choice available at each step in the hope that the overall best result can be achieved this way. By contrast, methods such as genetic algorithms and simulated annealing, discussed below, are not greedy; these methods sometimes make suboptimal choices in the hopes that they will lead to better solutions later on.
- Simulated annealing
Another optimization technique similar to evolutionary algorithms is known as simulated annealing. The idea borrows its name from the industrial process of annealing in which a material is heated to above its melting point, then gradually cooled in order to erase defects in its crystalline structure, producing a more stable and regular lattice arrangement of atoms (Haupt and Haupt 1998, p. 16). In simulated annealing, as in genetic algorithms, there is a fitness function that defines a fitness landscape; however, rather than a population of candidates as in GAs, there is only one candidate solution. Simulated annealing also adds the concept of "temperature", a global numerical quantity which gradually decreases over time. At each step of the algorithm, the solution mutates (which is equivalent to moving to an adjacent point of the fitness landscape). The fitness of the new solution is then compared to the fitness of the previous solution; if it is higher, the new solution is kept. Otherwise, the algorithm makes a decision whether to keep or discard it based on temperature. If the temperature is high, as it is initially, even changes that cause significant decreases in fitness may be kept and used as the basis for the next round of the algorithm, but as temperature decreases, the algorithm becomes more and more inclined to only accept fitness-increasing changes. Finally, the temperature reaches zero and the system "freezes"; whatever configuration it is in at that point becomes the solution. Simulated annealing is often used for engineering design applications such as determining the physical layout of components on a computer chip (Kirkpatrick, Gelatt and Vecchi 1983).
The earliest instances of what might today be called genetic algorithms appeared in the late 1950s and early 1960s, programmed on computers by evolutionary biologists who were explicitly seeking to model aspects of natural evolution. It did not occur to any of them that this strategy might be more generally applicable to artificial problems, but that recognition was not long in coming: "Evolutionary computation was definitely in the air in the formative days of the electronic computer" (Mitchell 1996, p.2). By 1962, researchers such as G.E.P. Box, G.J. Friedman, W.W. Bledsoe and H.J. Bremermann had all independently developed evolution-inspired algorithms for function optimization and machine learning, but their work attracted little followup. A more successful development in this area came in 1965, when Ingo Rechenberg, then of the Technical University of Berlin, introduced a technique he called evolution strategy, though it was more similar to hill-climbers than to genetic algorithms. In this technique, there was no population or crossover; one parent was mutated to produce one offspring, and the better of the two was kept and became the parent for the next round of mutation (Haupt and Haupt 1998, p.146). Later versions introduced the idea of a population. Evolution strategies are still employed today by engineers and scientists, especially in Germany.
The next important development in the field came in 1966, when L.J. Fogel, A.J. Owens and M.J. Walsh introduced in America a technique they called evolutionary programming. In this method, candidate solutions to problems were represented as simple finite-state machines; like Rechenberg's evolution strategy, their algorithm worked by randomly mutating one of these simulated machines and keeping the better of the two (Mitchell 1996, p.2; Goldberg 1989, p.105). Also like evolution strategies, a broader formulation of the evolutionary programming technique is still an area of ongoing research today. However, what was still lacking in both these methodologies was recognition of the importance of crossover.
As early as 1962, John Holland's work on adaptive systems laid the foundation for later developments; most notably, Holland was also the first to explicitly propose crossover and other recombination operators. However, the seminal work in the field of genetic algorithms came in 1975, with the publication of the book Adaptation in Natural and Artificial Systems. Building on earlier research and papers both by Holland himself and by colleagues at the University of Michigan, this book was the first to systematically and rigorously present the concept of adaptive digital systems using mutation, selection and crossover, simulating processes of biological evolution, as a problem-solving strategy. The book also attempted to put genetic algorithms on a firm theoretical footing by introducing the notion of schemata (Mitchell 1996, p.3; Haupt and Haupt 1998, p.147). That same year, Kenneth De Jong's important dissertation established the potential of GAs by showing that they could perform well on a wide variety of test functions, including noisy, discontinuous, and multimodal search landscapes (Goldberg 1989, p.107).
These foundational works established more widespread interest in evolutionary computation. By the early to mid-1980s, genetic algorithms were being applied to a broad range of subjects, from abstract mathematical problems like bin-packing and graph coloring to tangible engineering issues such as pipeline flow control, pattern recognition and classification, and structural optimization (Goldberg 1989, p. 128).
At first, these applications were mainly theoretical. However, as research continued to proliferate, genetic algorithms migrated into the commercial sector, their rise fueled by the exponential growth of computing power and the development of the Internet. Today, evolutionary computation is a thriving field, and genetic algorithms are "solving problems of everyday interest" (Haupt and Haupt 1998, p.147) in areas of study as diverse as stock market prediction and portfolio planning, aerospace engineering, microchip design, biochemistry and molecular biology, and scheduling at airports and assembly lines. The power of evolution has touched virtually any field one cares to name, shaping the world around us invisibly in countless ways, and new uses continue to be discovered as research is ongoing. And at the heart of it all lies nothing more than Charles Darwin's simple, powerful insight: that the random chance of variation, coupled with the law of selection, is a problem-solving technique of immense power and nearly unlimited application.
What are the strengths of GAs?
|
|
- The first and most important point is that genetic algorithms are intrinsically parallel. Most other algorithms are serial and can only explore the solution space to a problem in one direction at a time, and if the solution they discover turns out to be suboptimal, there is nothing to do but abandon all work previously completed and start over. However, since GAs have multiple offspring, they can explore the solution space in multiple directions at once. If one path turns out to be a dead end, they can easily eliminate it and continue work on more promising avenues, giving them a greater chance each run of finding the optimal solution.
However, the advantage of parallelism goes beyond this. Consider the following: All the 8-digit binary strings (strings of 0's and 1's) form a search space, which can be represented as ******** (where the * stands for "either 0 or 1"). The string 01101010 is one member of this space. However, it is also a member of the space 0*******, the space 01******, the space 0******0, the space 0*1*1*1*, the space 01*01**0, and so on. By evaluating the fitness of this one particular string, a genetic algorithm would be sampling each of these many spaces to which it belongs. Over many such evaluations, it would build up an increasingly accurate value for the average fitness of each of these spaces, each of which has many members. Therefore, a GA that explicitly evaluates a small number of individuals is implicitly evaluating a much larger group of individuals - just as a pollster who asks questions of a certain member of an ethnic, religious or social group hopes to learn something about the opinions of all members of that group, and therefore can reliably predict national opinion while sampling only a small percentage of the population. In the same way, the GA can "home in" on the space with the highest-fitness individuals and find the overall best one from that group. In the context of evolutionary algorithms, this is known as the Schema Theorem, and is the "central advantage" of a GA over other problem-solving methods (Holland 1992, p. 68; Mitchell 1996, p.28-29; Goldberg 1989, p.20).
- Due to the parallelism that allows them to implicitly evaluate many schema at once, genetic algorithms are particularly well-suited to solving problems where the space of all potential solutions is truly huge - too vast to search exhaustively in any reasonable amount of time. Most problems that fall into this category are known as "nonlinear". In a linear problem, the fitness of each component is independent, so any improvement to any one part will result in an improvement of the system as a whole. Needless to say, few real-world problems are like this. Nonlinearity is the norm, where changing one component may have ripple effects on the entire system, and where multiple changes that individually are detrimental may lead to much greater improvements in fitness when combined. Nonlinearity results in a combinatorial explosion: the space of 1,000-digit binary strings can be exhaustively searched by evaluating only 2,000 possibilities if the problem is linear, whereas if it is nonlinear, an exhaustive search requires evaluating 21000 possibilities - a number that would take over 300 digits to write out in full.
Fortunately, the implicit parallelism of a GA allows it to surmount even this enormous number of possibilities, successfully finding optimal or very good results in a short period of time after directly sampling only small regions of the vast fitness landscape (Forrest 1993, p. 877). For example, a genetic algorithm developed jointly by engineers from General Electric and Rensselaer Polytechnic Institute produced a high-performance jet engine turbine design that was three times better than a human-designed configuration and 50% better than a configuration designed by an expert system by successfully navigating a solution space containing more than 10387 possibilities. Conventional methods for designing such turbines are a central part of engineering projects that can take up to five years and cost over $2 billion; the genetic algorithm discovered this solution after two days on a typical engineering desktop workstation (Holland 1992, p.72).
- Another notable strength of genetic algorithms is that they perform well in problems for which the fitness landscape is complex - ones where the fitness function is discontinuous, noisy, changes over time, or has many local optima. Most practical problems have a vast solution space, impossible to search exhaustively; the challenge then becomes how to avoid the local optima - solutions that are better than all the others that are similar to them, but that are not as good as different ones elsewhere in the solution space. Many search algorithms can become trapped by local optima: if they reach the top of a hill on the fitness landscape, they will discover that no better solutions exist nearby and conclude that they have reached the best one, even though higher peaks exist elsewhere on the map.
Evolutionary algorithms, on the other hand, have proven to be effective at escaping local optima and discovering the global optimum in even a very rugged and complex fitness landscape. (It should be noted that, in reality, there is usually no way to tell whether a given solution to a problem is the one global optimum or just a very high local optimum. However, even if a GA does not always deliver a provably perfect solution to a problem, it can almost always deliver at least a very good solution.) All four of a GA's major components - parallelism, selection, mutation, and crossover - work together to accomplish this. In the beginning, the GA generates a diverse initial population, casting a "net" over the fitness landscape. (Koza (2003, p. 506) compares this to an army of parachutists dropping onto the landscape of a problem's search space, with each one being given orders to find the highest peak.) Small mutations enable each individual to explore its immediate neighborhood, while selection focuses progress, guiding the algorithm's offspring uphill to more promising parts of the solution space (Holland 1992, p. 68).
However, crossover is the key element that distinguishes genetic algorithms from other methods such as hill-climbers and simulated annealing. Without crossover, each individual solution is on its own, exploring the search space in its immediate vicinity without reference to what other individuals may have discovered. However, with crossover in place, there is a transfer of information between successful candidates - individuals can benefit from what others have learned, and schemata can be mixed and combined, with the potential to produce an offspring that has the strengths of both its parents and the weaknesses of neither. This point is illustrated in Koza et al. 1999, p.486, where the authors discuss a problem of synthesizing a lowpass filter using genetic programming. In one generation, two parent circuits were selected to undergo crossover; one parent had good topology (components such as inductors and capacitors in the right places) but bad sizing (values of inductance and capacitance for its components that were far too low). The other parent had bad topology, but good sizing. The result of mating the two through crossover was an offspring with the good topology of one parent and the good sizing of the other, resulting in a substantial improvement in fitness over both its parents.
The problem of finding the global optimum in a space with many local optima is also known as the dilemma of exploration vs. exploitation, "a classic problem for all systems that can adapt and learn" (Holland 1992, p. 69). Once an algorithm (or a human designer) has found a problem-solving strategy that seems to work satisfactorily, should it concentrate on making the best use of that strategy, or should it search for others? Abandoning a proven strategy to look for new ones is almost guaranteed to involve losses and degradation of performance, at least in the short term. But if one sticks with a particular strategy to the exclusion of all others, one runs the risk of not discovering better strategies that exist but have not yet been found. Again, genetic algorithms have shown themselves to be very good at striking this balance and discovering good solutions with a reasonable amount of time and computational effort.
- Another area in which genetic algorithms excel is their ability to manipulate many parameters simultaneously (Forrest 1993, p. 874). Many real-world problems cannot be stated in terms of a single value to be minimized or maximized, but must be expressed in terms of multiple objectives, usually with tradeoffs involved: one can only be improved at the expense of another. GAs are very good at solving such problems: in particular, their use of parallelism enables them to produce multiple equally good solutions to the same problem, possibly with one candidate solution optimizing one parameter and another candidate optimizing a different one (Haupt and Haupt 1998, p.17), and a human overseer can then select one of these candidates to use. If a particular solution to a multiobjective problem optimizes one parameter to a degree such that that parameter cannot be further improved without causing a corresponding decrease in the quality of some other parameter, that solution is called Pareto optimal or non-dominated (Coello 2000, p. 112).
- Finally, one of the qualities of genetic algorithms which might at first appear to be a liability turns out to be one of their strengths: namely, GAs know nothing about the problems they are deployed to solve. Instead of using previously known domain-specific information to guide each step and making changes with a specific eye towards improvement, as human designers do, they are "blind watchmakers" (Dawkins 1996); they make random changes to their candidate solutions and then use the fitness function to determine whether those changes produce an improvement.
The virtue of this technique is that it allows genetic algorithms to start out with an open mind, so to speak. Since its decisions are based on randomness, all possible search pathways are theoretically open to a GA; by contrast, any problem-solving strategy that relies on prior knowledge must inevitably begin by ruling out many pathways a priori, therefore missing any novel solutions that may exist there (Koza et al. 1999, p. 547). Lacking preconceptions based on established beliefs of "how things should be done" or what "couldn't possibly work", GAs do not have this problem. Similarly, any technique that relies on prior knowledge will break down when such knowledge is not available, but again, GAs are not adversely affected by ignorance (Goldberg 1989, p. 23). Through their components of parallelism, crossover and mutation, they can range widely over the fitness landscape, exploring regions which intelligently produced algorithms might have overlooked, and potentially uncovering solutions of startling and unexpected creativity that might never have occurred to human designers. One vivid illustration of this is the rediscovery, by genetic programming, of the concept of negative feedback - a principle crucial to many important electronic components today, but one that, when it was first discovered, was denied a patent for nine years because the concept was so contrary to established beliefs (Koza et al. 2003, p. 413). Evolutionary algorithms, of course, are neither aware nor concerned whether a solution runs counter to established beliefs - only whether it works.
What are the limitations of GAs?
|
|
Although genetic algorithms have proven to be an efficient and powerful problem-solving strategy, they are not a panacea. GAs do have certain limitations; however, it will be shown that all of these can be overcome and none of them bear on the validity of biological evolution.
- The first, and most important, consideration in creating a genetic algorithm is defining a representation for the problem. The language used to specify candidate solutions must be robust; i.e., it must be able to tolerate random changes such that fatal errors or nonsense do not consistently result.
There are two main ways of achieving this. The first, which is used by most genetic algorithms, is to define individuals as lists of numbers - binary-valued, integer-valued, or real-valued - where each number represents some aspect of a candidate solution. If the individuals are binary strings, 0 or 1 could stand for the absence or presence of a given feature. If they are lists of numbers, these numbers could represent many different things: the weights of the links in a neural network, the order of the cities visited in a given tour, the spatial placement of electronic components, the values fed into a controller, the torsion angles of peptide bonds in a protein, and so on. Mutation then entails changing these numbers, flipping bits or adding or subtracting random values. In this case, the actual program code does not change; the code is what manages the simulation and keeps track of the individuals, evaluating their fitness and perhaps ensuring that only values realistic and possible for the given problem result.
In another method, genetic programming, the actual program code does change. As discussed in the section Methods of representation, GP represents individuals as executable trees of code that can be mutated by changing or swapping subtrees. Both of these methods produce representations that are robust against mutation and can represent many different kinds of problems, and as discussed in the section Some specific examples, both have had considerable success.
This issue of representing candidate solutions in a robust way does not arise in nature, because the method of representation used by evolution, namely the genetic code, is inherently robust: with only a very few exceptions, such as a string of stop codons, there is no such thing as a sequence of DNA bases that cannot be translated into a protein. Therefore, virtually any change to an individual's genes will still produce an intelligible result, and so mutations in evolution have a higher chance of producing an improvement. This is in contrast to human-created languages such as English, where the number of meaningful words is small compared to the total number of ways one can combine letters of the alphabet, and therefore random changes to an English sentence are likely to produce nonsense.
- The problem of how to write the fitness function must be carefully considered so that higher fitness is attainable and actually does equate to a better solution for the given problem. If the fitness function is chosen poorly or defined imprecisely, the genetic algorithm may be unable to find a solution to the problem, or may end up solving the wrong problem. (This latter situation is sometimes described as the tendency of a GA to "cheat", although in reality all that is happening is that the GA is doing what it was told to do, not what its creators intended it to do.) An example of this can be found in Graham-Rowe 2002, in which researchers used an evolutionary algorithm in conjunction with a reprogrammable hardware array, setting up the fitness function to reward the evolving circuit for outputting an oscillating signal. At the end of the experiment, an oscillating signal was indeed being produced - but instead of the circuit itself acting as an oscillator, as the researchers had intended, they discovered that it had become a radio receiver that was picking up and relaying an oscillating signal from a nearby piece of electronic equipment!
This is not a problem in nature, however. In the laboratory of biological evolution there is only one fitness function, which is the same for all living things - the drive to survive and reproduce, no matter what adaptations make this possible. Those organisms which reproduce more abundantly compared to their competitors are more fit; those which fail to reproduce are unfit.
- In addition to making a good choice of fitness function, the other parameters of a GA - the size of the population, the rate of mutation and crossover, the type and strength of selection - must be also chosen with care. If the population size is too small, the genetic algorithm may not explore enough of the solution space to consistently find good solutions. If the rate of genetic change is too high or the selection scheme is chosen poorly, beneficial schema may be disrupted and the population may enter error catastrophe, changing too fast for selection to ever bring about convergence.
Living things do face similar difficulties, and evolution has dealt with them. It is true that if a population size falls too low, mutation rates are too high, or the selection pressure is too strong (such a situation might be caused by drastic environmental change), then the species may go extinct. The solution has been "the evolution of evolvability" - adaptations that alter a species' ability to adapt. For example, most living things have evolved elaborate molecular machinery that checks for and corrects errors during the process of DNA replication, keeping their mutation rate down to acceptably low levels; conversely, in times of severe environmental stress, some bacterial species enter a state of hypermutation where the rate of DNA replication errors rises sharply, increasing the chance that a compensating mutation will be discovered. Of course, not all catastrophes can be evaded, but the enormous diversity and highly complex adaptations of living things today show that, in general, evolution is a successful strategy. Likewise, the diverse applications of and impressive results produced by genetic algorithms show them to be a powerful and worthwhile field of study.
- One type of problem that genetic algorithms have difficulty dealing with are problems with "deceptive" fitness functions (Mitchell 1996, p.125), those where the locations of improved points give misleading information about where the global optimum is likely to be found. For example, imagine a problem where the search space consisted of all eight-character binary strings, and the fitness of an individual was directly proportional to the number of 1s in it - i.e., 00000001 would be less fit than 00000011, which would be less fit than 00000111, and so on - with two exceptions: the string 11111111 turned out to have very low fitness, and the string 00000000 turned out to have very high fitness. In such a problem, a GA (as well as most other algorithms) would be no more likely to find the global optimum than random search.
The resolution to this problem is the same for both genetic algorithms and biological evolution: evolution is not a process that has to find the single global optimum every time. It can do almost as well by reaching the top of a high local optimum, and for most situations, this will suffice, even if the global optimum cannot easily be reached from that point. Evolution is very much a "satisficer" - an algorithm that delivers a "good enough" solution, though not necessarily the best possible solution, given a reasonable amount of time and effort invested in the search. The Evidence for Jury-Rigged Design in Nature FAQ gives examples of this very outcome appearing in nature. (It is also worth noting that few, if any, real-world problems are as fully deceptive as the somewhat contrived example given above. Usually, the location of local improvements gives at least some information about the location of the global optimum.)
- One well-known problem that can occur with a GA is known as premature convergence. If an individual that is more fit than most of its competitors emerges early on in the course of the run, it may reproduce so abundantly that it drives down the population's diversity too soon, leading the algorithm to converge on the local optimum that that individual represents rather than searching the fitness landscape thoroughly enough to find the global optimum (Forrest 1993, p. 876; Mitchell 1996, p. 167). This is an especially common problem in small populations, where even chance variations in reproduction rate may cause one genotype to become dominant over others.
The most common methods implemented by GA researchers to deal with this problem all involve controlling the strength of selection, so as not to give excessively fit individuals too great of an advantage. Rank, scaling and tournament selection, discussed earlier, are three major means for accomplishing this; some methods of scaling selection include sigma scaling, in which reproduction is based on a statistical comparison to the population's average fitness, and Boltzmann selection, in which the strength of selection increases over the course of a run in a manner similar to the "temperature" variable in simulated annealing (Mitchell 1996, p. 168).
Premature convergence does occur in nature (where it is called genetic drift by biologists). This should not be surprising; as discussed above, evolution as a problem-solving strategy is under no obligation to find the single best solution, merely one that is good enough. However, premature convergence in nature is less common since most beneficial mutations in living things produce only small, incremental fitness improvements; mutations that produce such a large fitness gain as to give their possessors dramatic reproductive advantage are rare.
- Finally, several researchers (Holland 1992, p.72; Forrest 1993, p.875; Haupt and Haupt 1998, p.18) advise against using genetic algorithms on analytically solvable problems. It is not that genetic algorithms cannot find good solutions to such problems; it is merely that traditional analytic methods take much less time and computational effort than GAs and, unlike GAs, are usually mathematically guaranteed to deliver the one exact solution. Of course, since there is no such thing as a mathematically perfect solution to any problem of biological adaptation, this issue does not arise in nature.
Some specific examples of GAs
|
|
As the power of evolution gains increasingly widespread recognition, genetic algorithms have been used to tackle a broad variety of problems in an extremely diverse array of fields, clearly showing their power and their potential. This section will discuss some of the more noteworthy uses to which they have been put.
- Acoustics
Sato et al. 2002 used genetic algorithms to design a concert hall with optimal acoustic properties, maximizing the sound quality for the audience, for the conductor, and for the musicians on stage. This task involves the simultaneous optimization of multiple variables. Beginning with a shoebox-shaped hall, the authors' GA produced two non-dominated solutions, both of which were described as "leaf-shaped" (p.526). The authors state that these solutions have proportions similar to Vienna's Grosser Musikvereinsaal, which is widely agreed to be one of the best - if not the best - concert hall in the world in terms of acoustic properties.
Porto, Fogel and Fogel 1995 used evolutionary programming to train neural networks to distinguish between sonar reflections from different types of objects: man-made metal spheres, sea mounts, fish and plant life, and random background noise. After 500 generations, the best evolved neural network had a probability of correct classification ranging between 94% and 98% and a probability of misclassification between 7.4% and 1.5%, which are "reasonable probabilities of detection and false alarm" (p.21). The evolved network matched the performance of another network developed by simulated annealing and consistently outperformed networks trained by back propagation, which "repeatedly stalled at suboptimal weight sets that did not yield satisfactory results" (p.21). By contrast, both stochastic methods showed themselves able to overcome these local optima and produce smaller, effective and more robust networks; but the authors suggest that the evolutionary algorithm, unlike simulated annealing, operates on a population and so takes advantage of global information about the search space, potentially leading to better performance in the long run.
Tang et al. 1996 survey the uses of genetic algorithms within the field of acoustics and signal processing. One area of particular interest involves the use of GAs to design Active Noise Control (ANC) systems, which cancel out undesired sound by producing sound waves that destructively interfere with the unwanted noise. This is a multiple-objective problem requiring the precise placement and control of multiple loudspeakers; GAs have been used both to design the controllers and find the optimal placement of the loudspeakers for such systems, resulting in the "effective attenuation of noise" (p.33) in experimental tests.
- Aerospace engineering
Obayashi et al. 2000 used a multiple-objective genetic algorithm to design the wing shape for a supersonic aircraft. Three major considerations govern the wing's configuration - minimizing aerodynamic drag at supersonic cruising speeds, minimizing drag at subsonic speeds, and minimizing aerodynamic load (the bending force on the wing). These objectives are mutually exclusive, and optimizing them all simultaneously requires tradeoffs to be made.
The chromosome in this problem is a string of 66 real-valued numbers, each of which corresponds to a specific aspect of the wing: its shape, its thickness, its twist, and so on. Evolution with elitist rank selection was simulated for 70 generations, with a population size of 64 individuals. At the termination of this process, there were several Pareto-optimal individuals, each one representing a single non-dominated solution to the problem. The paper notes that these best-of-run individuals have "physically reasonable" characteristics, indicating the validity of the optimization technique (p.186). To further evaluate the quality of the solutions, six of the best were compared to a supersonic wing design produced by the SST Design Team of Japan's National Aerospace Laboratory. All six were competitive, having drag and load values approximately equal to or less than the human-designed wing; one of the evolved solutions in particular outperformed the NAL's design in all three objectives. The authors note that the GA's solutions are similar to a design called the "arrow wing" which was first suggested in the late 1950s, but ultimately abandoned in favor of the more conventional delta-wing design.
In a follow-up paper (Sasaki et al. 2001), the authors repeat their experiment while adding a fourth objective, namely minimizing the twisting moment of the wing (a known potential problem for arrow-wing SST designs). Additional control points for thickness are also added to the array of design variables. After 75 generations of evolution, two of the best Pareto-optimal solutions were again compared to the Japanese National Aerospace Laboratory's wing design for the NEXST-1 experimental supersonic airplane. It was found that both of these designs (as well as one optimal design from the previous simulation, discussed above) were physically reasonable and superior to the NAL's design in all four objectives.
Williams, Crossley and Lang 2001 applied genetic algorithms to the task of spacing satellite orbits to minimize coverage blackouts. As telecommunications technology continues to improve, humans are increasingly dependent on Earth-orbiting satellites to perform many vital functions, and one of the problems engineers face is designing their orbital trajectories. Satellites in high Earth orbit, around 22,000 miles up, can see large sections of the planet at once and be in constant contact with ground stations, but these are far more expensive to launch and more vulnerable to cosmic radiation. It is more economical to put satellites in low orbits, as low as a few hundred miles in some cases, but because of the curvature of the Earth it is inevitable that these satellites will at times lose line-of-sight access to surface receivers and thus be useless. Even constellations of several satellites experience unavoidable blackouts and losses of coverage for this reason. The challenge is to arrange the satellites' orbits to minimize this downtime. This is a multi-objective problem, involving the minimization of both the average blackout time for all locations and the maximum blackout time for any one location; in practice, these goals turn out to be mutually exclusive.
When the GA was applied to this problem, the evolved results for three, four and five-satellite constellations were unusual, highly asymmetric orbit configurations, with the satellites spaced by alternating large and small gaps rather than equal-sized gaps as conventional techniques would produce. However, this solution significantly reduced both average and maximum revisit times, in some cases by up to 90 minutes. In a news article about the results, Dr. William Crossley noted that "engineers with years of aerospace experience were surprised by the higher performance offered by the unconventional design".
| Keane and Brown 1996 used a GA to evolve a new design for a load-bearing truss or boom that could be assembled in orbit and used for satellites, space stations and other aerospace construction projects. The result, a twisted, organic-looking structure that has been compared to a human leg bone, uses no more material than the standard truss design but is lightweight, strong and far superior at damping out damaging vibrations, as was confirmed by real-world tests of the final product. And yet "No intelligence made the designs. They just evolved" (Petit 1998). The authors of the paper further note that their GA only ran for 10 generations due to the computationally intensive nature of the simulation, and the population had not become stagnant. Continuing the run for more generations would undoubtedly have produced further improvements in performance. |
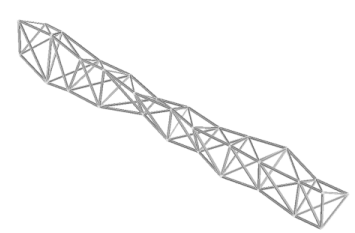
Figure 4: A genetically optimized three-dimensional truss with improved frequency response. (Adapted from [1].) |
Finally, as reported in Gibbs 1996, Lockheed Martin has used a genetic algorithm to evolve a series of maneuvers to shift a spacecraft from one orientation to another within 2% of the theoretical minimum time for such maneuvers. The evolved solution was 10% faster than a solution hand-crafted by an expert for the same problem.
- Astronomy and astrophysics
Charbonneau 1995 suggests the usefulness of GAs for problems in astrophysics by applying them to three example problems: fitting the rotation curve of a galaxy based on observed rotational velocities of its components, determining the pulsation period of a variable star based on time-series data, and solving for the critical parameters in a magnetohydrodynamic model of the solar wind. All three of these are hard multi-dimensional nonlinear problems.
Charbonneau's genetic algorithm, PIKAIA, uses generational, fitness-proportionate ranking selection coupled with elitism, ensuring that the single best individual is copied over once into the next generation without modification. PIKAIA has a crossover rate of 0.65 and a variable mutation rate that is set to 0.003 initially and gradually increases later on, as the population approaches convergence, to maintain variability in the gene pool.
In the galactic rotation-curve problem, the GA produced two curves, both of which were very good fits to the data (a common result in this type of problem, in which there is little contrast between neighboring hilltops); further observations can then distinguish which one is to be preferred. In the time-series problem, the GA was impressively successful in autonomously generating a high-quality fit for the data, but harder problems were not fitted as well (although, Charbonneau points out, these problems are equally difficult to solve with conventional techniques). The paper suggests that a hybrid GA employing both artificial evolution and standard analytic techniques might perform better. Finally, in solving for the six critical parameters of the solar wind, the GA successfully determined the value of three of them to an accuracy of within 0.1% and the remaining three to accuracies of within 1 to 10%. (Though lower experimental error for these three would always be preferable, Charbonneau notes that there are no other robust, efficient methods for experimentally solving a six-dimensional nonlinear problem of this type; a conjugate gradient method works "as long as a very good starting guess can be provided" (p.323). By contrast, GAs do not require such finely tuned domain-specific knowledge.)
Based on the results obtained so far, Charbonneau suggests that GAs can and should find use in other difficult problems in astrophysics, in particular inverse problems such as Doppler imaging and helioseismic inversions. In closing, Charbonneau argues that GAs are a "strong and promising contender" (p.324) in this field, one that can be expected to complement rather than replace traditional optimization techniques, and concludes that "the bottom line, if there is to be one, is that genetic algorithms work, and often frightfully well" (p.325).
- Chemistry
High-powered, ultrashort pulses of laser energy can split apart complex molecules into simpler molecules, a process with important applications to organic chemistry and microelectronics. The specific end products of such a reaction can be controlled by modulating the phase of the laser pulse. However, for large molecules, solving for the desired pulse shape analytically is too difficult: the calculations are too complex and the relevant characteristics (the potential energy surfaces of the molecules) are not known precisely enough.
Assion et al. 1998 solved this problem by using an evolutionary algorithm to design the pulse shape. Instead of inputting complex, problem-specific knowledge about the quantum characteristics of the input molecules to design the pulse to specifications, the EA fires a pulse, measures the proportions of the resulting product molecules, randomly mutates the beam characteristics with the hope of getting these proportions closer to the desired output, and the process repeats. (Rather than fine-tune any characteristics of the laser beam directly, the authors' GA represents individuals as a set of 128 numbers, each of which is a voltage value that controls the refractive index of one of the pixels in the laser light modulator. Again, no problem-specific knowledge about the properties of either the laser or the reaction products is needed.) The authors state that their algorithm, when applied to two sample substances, "automatically finds the best configuration... no matter how complicated the molecular response may be" (p.920), demonstrating "automated coherent control on products that are chemically different from each other and from the parent molecule" (p.921).
In the early to mid-1990s, the widespread adoption of a novel drug design technique called combinatorial chemistry revolutionized the pharmaceutical industry. In this method, rather than the painstaking, precise synthesis of a single compound at a time, biochemists deliberately mix a wide variety of reactants to produce an even wider variety of products - hundreds, thousands or millions of different compounds per batch - which can then be rapidly screened for biochemical activity. In designing libraries of reactants for this technique, there are two main approaches: reactant-based design, which chooses optimized groups of reactants without considering what products will result, and product-based design, which selects reactants most likely to produce products with the desired properties. Product-based design is more difficult and complex, but has been shown to result in better and more diverse combinatorial libraries and a greater likelihood of getting a usable result.
In a paper funded by GlaxoSmithKline's research and development department, Gillet 2002 discusses the use of a multiobjective genetic algorithm for the product-based design of combinatorial libraries. In choosing the compounds that go into a particular library, qualities such as molecular diversity and weight, cost of supplies, toxicity, absorption, distribution, and metabolism must all be considered. If the aim is to find molecules similar to an existing molecule of known function (a common method of new drug design), structural similarity can also be taken into account. This paper presents a multiobjective approach where a set of Pareto-optimal results that maximize or minimize each of these objectives can be developed. The author concludes that the GA was able to simultaneously satisfy the criteria of molecular diversity and maximum synthetic efficiency, and was able to find molecules that were drug-like as well as "very similar to given target molecules after exploring a very small fraction of the total search space" (p.378).
In a related paper, Glen and Payne 1995 discuss the use of genetic algorithms to automatically design new molecules from scratch to fit a given set of specifications. Given an initial population either generated randomly or using the simple molecule ethane as a seed, the GA randomly adds, removes and alters atoms and molecular fragments with the aim of generating molecules that fit the given constraints. The GA can simultaneously optimize a large number of objectives, including molecular weight, molecular volume, number of bonds, number of chiral centers, number of atoms, number of rotatable bonds, polarizability, dipole moment, and more in order to produce candidate molecules with the desired properties. Based on experimental tests, including one difficult optimization problem that involved generating molecules with properties similar to ribose (a sugar compound frequently mimicked in antiviral drugs), the authors conclude that the GA is an "excellent idea generator" (p.199) that offers "fast and powerful optimisation properties" and can generate "a diverse set of possible structures" (p.182). They go on to state, "Of particular note is the powerful optimising ability of the genetic algorithm, even with relatively small population sizes" (p.200). In a sign that these results are not merely theoretical, Lemley 2001 reports that the Unilever corporation has used genetic algorithms to design new antimicrobial compounds for use in cleansers, which it has patented.
- Electrical engineering
A field-programmable gate array, or FPGA for short, is a special type of circuit board with an array of logic cells, each of which can act as any type of logic gate, connected by flexible interlinks which can connect cells. Both of these functions are controlled by software, so merely by loading a special program into the board, it can be altered on the fly to perform the functions of any one of a vast variety of hardware devices.
Dr. Adrian Thompson has exploited this device, in conjunction with the principles of evolution, to produce a prototype voice-recognition circuit that can distinguish between and respond to spoken commands using only 37 logic gates - a task that would have been considered impossible for any human engineer. He generated random bit strings of 0s and 1s and used them as configurations for the FPGA, selecting the fittest individuals from each generation, reproducing and randomly mutating them, swapping sections of their code and passing them on to another round of selection. His goal was to evolve a device that could at first discriminate between tones of different frequencies (1 and 10 kilohertz), then distinguish between the spoken words "go" and "stop".
This aim was achieved within 3000 generations, but the success was even greater than had been anticipated. The evolved system uses far fewer cells than anything a human engineer could have designed, and it does not even need the most critical component of human-built systems - a clock. How does it work? Thompson has no idea, though he has traced the input signal through a complex arrangement of feedback loops within the evolved circuit. In fact, out of the 37 logic gates the final product uses, five of them are not even connected to the rest of the circuit in any way - yet if their power supply is removed, the circuit stops working. It seems that evolution has exploited some subtle electromagnetic effect of these cells to come up with its solution, yet the exact workings of the complex and intricate evolved structure remain a mystery (Davidson 1997).
Altshuler and Linden 1997 used a genetic algorithm to evolve wire antennas with pre-specified properties. The authors note that the design of such antennas is an imprecise process, starting with the desired properties and then determining the antenna's shape through "guesses.... intuition, experience, approximate equations or empirical studies" (p.50). This technique is time-consuming, often does not produce optimal results, and tends to work well only for relatively simple, symmetric designs. By contrast, in the genetic algorithm approach, the engineer specifies the antenna's electromagnetic properties, and the GA automatically synthesizes a matching configuration.

Figure 5: A crooked-wire genetic antenna
(after Altshuler and Linden 1997, figure 1). |
Altshuler and Linden used their GA to design a circularly polarized seven-segment antenna with hemispherical coverage; the result is shown to the left. Each individual in the GA consisted of a binary chromosome specifying the three-dimensional coordinates of each end of each wire. Fitness was evaluated by simulating each candidate according to an electromagnetic wiring code, and the best-of-run individual was then built and tested. The authors describe the shape of this antenna, which does not resemble traditional antennas and has no obvious symmetry, as "unusually weird" and "counter-intuitive" (p.52), yet it had a nearly uniform radiation pattern with high bandwidth both in simulation and in experimental testing, excellently matching the prior specification. The authors conclude that a genetic algorithm-based method for antenna design shows "remarkable promise". "...this new design procedure is capable of finding genetic antennas able to effectively solve difficult antenna problems, and it will be particularly useful in situations where existing designs are not adequate" (p.52). |
- Financial markets
Mahfoud and Mani 1996 used a genetic algorithm to predict the future performance of 1600 publicly traded stocks. Specifically, the GA was tasked with forecasting the relative return of each stock, defined as that stock's return minus the average return of all 1600 stocks over the time period in question, 12 weeks (one calendar quarter) into the future. As input, the GA was given historical data about each stock in the form of a list of 15 attributes, such as price-to-earnings ratio and growth rate, measured at various past points in time; the GA was asked to evolve a set of if/then rules to classify each stock and to provide, as output, both a recommendation on what to do with regards to that stock (buy, sell, or no prediction) and a numerical forecast of the relative return. The GA's results were compared to those of an established neural net-based system which the authors had been using to forecast stock prices and manage portfolios for three years previously. Of course, the stock market is an extremely noisy and nonlinear system, and no predictive mechanism can be correct 100% of the time; the challenge is to find a predictor that is accurate more often than not.
In the experiment, the GA and the neural net each made forecasts at the end of the week for each one of the 1600 stocks, for twelve consecutive weeks. Twelve weeks after each prediction, the actual performance was compared with the predicted relative return. Overall, the GA significantly outperformed the neural network: in one trial run, the GA correctly predicted the direction of one stock 47.6% of the time, made no prediction 45.8% of the time, and made an incorrect prediction only 6.6% of the time, for an overall predictive accuracy of 87.8%. Although the neural network made definite predictions more often, it was also wrong in its predictions more often (in fact, the authors speculate that the GA's greater ability to make no prediction when the data were uncertain was a factor in its success; the neural net always produces a prediction unless explicitly restricted by the programmer). In the 1600-stock experiment, the GA produced a relative return of +5.47%, versus +4.40% for the neural net - a statistically significant difference. In fact, the GA also significantly outperformed three major stock market indices - the S&P 500, the S&P 400, and the Russell 2000 - over this period; chance was excluded as the cause of this result at the 95% confidence level. The authors attribute this compelling success to the ability of the genetic algorithm to learn nonlinear relationships not readily apparent to human observers, as well as the fact that it lacks a human expert's "a priori bias against counterintuitive or contrarian rules" (p.562).
Similar success was achieved by Andreou, Georgopoulos and Likothanassis 2002, who used hybrid genetic algorithms to evolve neural networks that predicted the exchange rates of foreign currencies up to one month ahead. As opposed to the last example, where GAs and neural nets were in competition, here the two worked in concert, with the GA evolving the architecture (number of input units, number of hidden units, and the arrangement of the links between them) of the network which was then trained by a filter algorithm.
As historical information, the algorithm was given 1300 previous raw daily values of five currencies - the American dollar, the German deutsche mark, the French franc, the British pound, and the Greek drachma - and asked to predict their future values 1, 2, 5, and 20 days ahead. The hybrid GA's performance, in general, showed a "remarkable level of accuracy" (p.200) in all cases tested, outperforming several other methods including neural networks alone. Correlations for the one-day case ranged from 92 to 99%, and though accuracy decreased over increasingly greater time lags, the GA continued to be "quite successful" (p.206) and clearly outperformed the other methods. The authors conclude that "remarkable prediction success has been achieved in both a one-step ahead and a multistep predicting horizon" (p.208) - in fact, they state that their results are better by far than any related predictive strategies attempted on this data series or other currencies.
The uses of GAs on the financial markets have begun to spread into real-world brokerage firms. Naik 1996 reports that LBS Capital Management, an American firm headquartered in Florida, uses genetic algorithms to pick stocks for a pension fund it manages. Coale 1997 and Begley and Beals 1995 report that First Quadrant, an investment firm in California that manages over $2.2 billion, uses GAs to make investment decisions for all of their financial services. Their evolved model earns, on average, $255 for every $100 invested over six years, as opposed to $205 for other types of modeling systems.
- Game playing
One of the most novel and compelling demonstrations of the power of genetic algorithms was presented by Chellapilla and Fogel 2001, who used a GA to evolve neural networks that could play the game of checkers. The authors state that one of the major difficulties in these sorts of strategy-related problems is the credit assignment problem - in other words, how does one write a fitness function? It has been widely believed that the mere criterion of win, lose or draw does not provide sufficient information for an evolutionary algorithm to figure out what constitutes good play.
In this paper, Chellapilla and Fogel overturn that assumption. Given only the spatial positions of pieces on the checkerboard and the total number of pieces possessed by each side, they were able to evolve a checkers program that plays at a level competitive with human experts, without any intelligent input as to what constitutes good play - indeed, the individuals in the evolutionary algorithm were not even told what the criteria for a win were, nor were they told the result of any one game.
In Chellapilla and Fogel's representation, the game state was represented by a numeric list of 32 elements, with each position in the list corresponding to an available position on the board. The value at each position was either 0 for an unoccupied square, -1 if that square was occupied by an enemy checker, +1 if that square was occupied by one of the program's checkers, and -K or +K for a square occupied by an enemy or friendly king. (The value of K was not pre-specified, but again was determined by evolution over the course of the algorithm.) Accompanying this was a neural network with multiple processing layers and one input layer with a node for each of the possible 4x4, 5x5, 6x6, 7x7 and 8x8 squares on the board. The output of the neural net for any given arrangement of pieces was a value from -1 to +1 indicating how good it felt that position was for it. For each move, the neural network was presented with a game tree listing all possible moves up to four turns into the future, and a move decision was made based on which branch of the tree produced the best results for it.
The evolutionary algorithm began with a population of 15 neural networks with randomly generated weights and biases assigned to each node and link; each individual then reproduced once, generating an offspring with variations in the values of the network. These 30 individuals then competed for survival by playing against each other, with each individual competing against 5 randomly chosen opponents per turn. 1 point was awarded for each win and 2 points were deducted for each loss. The 15 best performers, based on total score, were selected to produce offspring for the next generation, and the process repeated. Evolution was continued for 840 generations (approximately six months of computer time).
| Class |
Rating |
| Senior Master |
2400+ |
| Master |
2200-2399 |
| Expert |
2000-2199 |
| Class A |
1800-1999 |
| Class B |
1600-1799 |
| Class C |
1400-1599 |
| Class J |
< 200 |
|
The single best individual that emerged from this selection was entered as a competitor on the gaming website http://www.zone.com/. Over a period of two months, it played against 165 human opponents comprising a range of high skill levels, from class C to master, according to the ranking system of the United States Chess Federation (shown at left, some ranks omitted for clarity). Of these games, the neural net won 94, lost 39 and drew 32; based on the rankings of the opponents in these games, the evolved neural net was equivalent to a player with a mean rating of 2045.85, placing it at the expert level - a higher ranking than 99.61% of over 80,000 players registered at the website. One of the neural net's most significant victories was when it defeated a player ranked 98th out of all registered players, whose rating was just 27 points below master level. |
Tests conducted with a simple piece-differential program (which bases moves solely on the difference between the number of checkers remaining to each side) with an eight-move look-ahead showed the neural net to be significantly superior, with a rating over 400 points higher. "A program that relies only on the piece count and an eight-ply search will defeat a lot of people, but it is not an expert. The best evolved neural network is" (p.425). Even when it was searching positions two further moves ahead than the neural net, the piece-differential program lost decisively in eight out of ten games. This conclusively demonstrates that the evolved neural net is not merely counting pieces, but is somehow processing spatial characteristics of the board to decide its moves. The authors point out that opponents on zone.com often commented that the neural net's moves were "strange", but its overall level of play was described as "very tough" or with similar complimentary terms.
To further test the evolved neural network (which the authors named "Anaconda" since it often won by restricting its opponents' mobility), it was played against a commercial checkers program, Hoyle's Classic Games, distributed by Sierra Online (Chellapilla and Fogel 2000). This program comes with a variety of built-in characters, each of whom plays at a different skill level. Anaconda was tested against three characters ("Beatrice", "Natasha" and "Leopold") designated as expert-level players, playing one game as red and one game as white against each of them with a six-ply look-ahead. Though the authors doubted that this depth of look-ahead would give Anaconda the ability to play at the expert skill level it had previously shown, it won six straight victories out of all six games played. Based on this outcome, the authors expressed skepticism over whether the Hoyle software played at the skill level advertised, though it should be noted that they reached this conclusion based solely on the ease with which Anaconda defeated it!
The ultimate test of Anaconda was given in Chellapilla and Fogel 2002, where the evolved neural net was matched against the best checkers player in the world: Chinook, a program designed principally by Dr. Jonathan Schaeffer of the University of Alberta. Rated at 2814 in 1996 (with its closest human competitors rated in the 2600s), Chinook incorporates a book of opening moves provided by human grandmasters, a sophisticated set of middle-game algorithms, and a complete database of all possible moves with ten pieces on the board or less, so it never makes a mistake in the endgame. An enormous amount of human intelligence and expertise went into the design of this program.
Chellapilla and Fogel pitted Anaconda against Chinook in a 10-game tournament, with Chinook playing at a 5-ply skill level, making it roughly approximate to master level. Chinook won this contest, four wins to two with four draws. (Interestingly, the authors note, in two of the games that ended as draws, Anaconda held the lead with four kings to Chinook's three. Furthermore, one of Chinook's wins came from a 10-ply series of movies drawn from its endgame database, which Anaconda with an 8-ply look-ahead could not have anticipated. If Anaconda had had access to an endgame database of the same quality as Chinook's, the outcome of the tournament might well have been a victory for Anaconda, four wins to three.) These results "provide good support for the expert-level rating that Anaconda earned on www.zone.com" (p.76), with an overall rating of 2030-2055, comparable to the 2045 rating it earned by playing against humans. While Anaconda is not an invulnerable player, it is able to play competitively at the expert level and hold its own against a variety of extremely skilled human checkers players. When one considers the very simple fitness criterion under which these results were obtained, the emergence of Anaconda provides dramatic corroboration of the power of evolution.
- Geophysics
Sambridge and Gallagher 1993 used a genetic algorithm to locate earthquake hypocenters based on seismological data. (The hypocenter is the point beneath the Earth's surface at which an earthquake begins. The epicenter is the point on the surface directly above the hypocenter.) This is an exceedingly complex task, since the properties of seismic waves depend on the properties of the rock layers through which they travel. The traditional method for locating the hypocenter relies upon what is known as a seismic inversion algorithm, which starts with a best guess of the location, calculates the derivatives of wave travel time with respect to source position, and performs a matrix operation to provide an updated location. This process is repeated until an acceptable solution is reached. (This Post of the Month, from November 2003, provides more information.) However, this method requires derivative information and is prone to becoming trapped on local optima.
A location algorithm that does not depend on derivative information or velocity models can avoid these shortfalls by calculating only the forward problem - the difference between observed and predicted wave arrival times for different hypocenter locations. However, an exhaustive search based on this method would be far too computationally expensive. This, of course, is precisely the type of optimization problem at which genetic algorithms excel. Like all GAs, the one proposed by the cited paper is parallel in nature - rather than progressively perturbing a single hypocenter closer and closer to the solution, it begins with a cloud of potential hypocenters which shrinks over time to converge on a single solution. The authors state that their approach "can rapidly locate near optimal solutions without an exhaustive search of the parameter space" (p.1467), displays "highly organized behavior resulting in efficient search" and is "a compromise between the efficiency of derivative based methods and the robustness of a fully nonlinear exhaustive search" (p.1469). The authors conclude that their genetic algorithm is "efficient for truly global optimization" (p.1488) and "a powerful new tool for performing robust hypocenter location" (p.1489).
- Materials engineering
Giro, Cyrillo and Galvão 2002 used genetic algorithms to design electrically conductive carbon-based polymers known as polyanilines. These polymers, a recently invented class of synthetic materials, have "large technological potential applications" and may open up windows onto "new fundamental physical phenomena" (p.170). However, due to their high reactivity, carbon atoms can form a virtually infinite number of structures, making a systematic search for new molecules with interesting properties all but impossible. In this paper, the authors apply a GA-based approach to the task of designing new molecules with pre-specified properties, starting with a randomly generated population of initial candidates. They conclude that their methodology can be a "very effective tool" (p.174) to guide experimentalists in the search for new compounds and is general enough to be extended to the design of novel materials belonging to virtually any class of molecules.
Weismann, Hammel and Bäck 1998 applied evolutionary algorithms to a "nontrivial" (p.162) industrial problem: the design of multilayer optical coatings used for filters that reflect, transmit or absorb light of specified frequencies. These coatings are used in the manufacture of sunglasses, for example, or compact discs. Their manufacture is a precise task: the layers must be laid down in a particular sequence and particular thicknesses to produce the desired result, and uncontrollable environmental variations in the manufacturing environment such as temperature, pollution and humidity may affect the performance of the finished product. Many local optima are not robust against such variations, meaning that maximum product quality must be paid for with higher rates of undesirable deviation. The particular problem considered in this paper also had multiple criteria: in addition to the reflectance, the spectral composition (color) of the reflected light was also considered.
The EA operated by varying the number of coating layers and the thickness of each, and produced designs that were "substantially more robust to parameter variation" (p.166) and had higher average performance than traditional methods. The authors conclude that "evolutionary algorithms can compete with or even outperform traditional methods" (p.167) of multilayer optical coating design, without having to incorporate domain-specific knowledge into the search function and without having to seed the population with good initial designs.
One more use of GAs in the field of materials engineering merits mention: Robin et al. 2003 used GAs to design exposure patterns for an electron lithography beam, used to etch submicrometer-scale structures onto integrated circuits. Designing these patterns is a highly difficult task; it is cumbersome and wasteful to determine them experimentally, but the high dimensionality of the search space defeats most search algorithms. As many as 100 parameters must be optimized simultaneously to control the electron beam and prevent scattering and proximity effects that would otherwise ruin the fine structures being sculpted. The forward problem - determining the resulting structure as a function of the electron dose - is straightforward and easy to simulate, but the inverse problem of determining the electron dose to produce a given structure, which is what is being solved here, is far harder and no deterministic solution exists.
Genetic algorithms, which are "known to be able to find good solutions to very complex problems of high dimensionality" (p.75) without needing to be supplied with domain-specific information on the topology of the search landscape, were applied successfully to this problem. The paper's authors employed a steady-state GA with roulette-wheel selection in a computer simulation, which yielded "very good optimized" (p.77) exposure patterns. By contrast, a type of hill-climber known as a simplex-downhill algorithm was applied to the same problem, without success; the SD method quickly became trapped in local optima which it could not escape, yielding solutions of poor quality. A hybrid approach of the GA and SD methods also could not improve on the results delivered by the GA alone.
- Mathematics and algorithmics
Although some of the most promising applications and compelling demonstrations of GAs' power are in the field of engineering design, they are also relevant to "pure" mathematical problems. Haupt and Haupt 1998 (p.140) discuss the use of GAs to solve high-order nonlinear partial differential equations, typically by finding the values for which the equations equal zero, and give as an example a near-perfect GA solution for the coefficients of the fifth-order Super Korteweg-de Vries equation.
Sorting a list of items into order is an important task in computer science, and a sorting network is an efficient way to accomplish this. A sorting network is a fixed list of comparisons performed on a set of a given size; in each comparison, two elements are compared and exchanged if not in order. Koza et al. 1999, p. 952 used genetic programming to evolve minimal sorting networks for 7-item sets (16 comparisons), 8-item sets (19 comparisons), and 9-item sets (25 comparisons). Mitchell 1996, p.21, discusses the use of genetic algorithms by W. Daniel Hillis to find a 61-comparison sorting network for a 16-item set, only one step more than the smallest known. This latter example is particularly interesting for two innovations it used: diploid chromosomes, and more notably, host-parasite coevolution. Both the sorting networks and the test cases evolved alongside each other; sorting networks were given higher fitness based on how many test cases they sorted correctly, while test cases were given higher fitness based on how many sorting networks they could "trick" into sorting incorrectly. The GA with coevolution performed significantly better than the same GA without it.
One final, noteworthy example of GAs in the field of algorithmics can be found in Koza et al. 1999, who used genetic programming to discover a rule for the majority classification problem in one-dimensional cellular automata that is better than all known rules written by humans. A one-dimensional cellular automaton can be thought of as a finite tape with a given number of positions (cells) on it, each of which can hold either the state 0 or the state 1. The automaton runs for a given number of time steps; at each step, every cell acquires a new value based on its previous value and the value of its nearest neighbors. (The Game of Life is a two-dimensional cellular automaton.) The majority classification problem entails finding a table of rules such that, if more than half the cells on the tape are 1 initially, all the cells go to 1; otherwise all the cells go to 0. The challenge lies in the fact that any individual cell can only access information about its nearest neighbors; therefore, good rule sets must somehow find a way to transmit information about distant regions of the tape.
It is known that a perfect solution to this problem does not exist - no rule set can accurately classify all possible initial configurations - but over the past twenty years, there has been a long succession of increasingly better solutions. In 1978, three researchers developed the so-called GKL rule, which correctly classifies 81.6% of the possible initial states. In 1993, a better rule with an accuracy of 81.8% was discovered; in 1995, another rule with accuracy of 82.178% was found. All of these rules required significant work by intelligent, creative humans to develop. By contrast, the best rule discovered by a run of genetic programming, given in Koza et al. 1999, p.973, has an overall accuracy of 82.326% - better than any of the human-created solutions that have been developed over the last two decades. The authors note that their new rules are qualitatively different from previously published rules, employing fine-grained internal representations of state density and intricate sets of signals for communicating information over long distance.
- Military and law enforcement
Kewley and Embrechts 2002 used genetic algorithms to evolve tactical plans for military battles. The authors note that "[p]lanning for a tactical military battle is a complex, high-dimensional task which often bedevils experienced professionals" (p.163), not only because such decisions are usually made under high-stress conditions, but also because even simple plans require a great number of conflicting variables and outcomes to take into account: minimizing friendly casualties, maximizing enemy casualties, controlling desired terrain, conserving resources, and so on. Human planners have difficulty dealing with the complexities of this task and often must resort to "quick and dirty" approaches, such as doing whatever worked last time.
To overcome these difficulties, the authors of the cited paper developed a genetic algorithm to automate the creation of battle plans, in conjunction with a graphical battle simulator program. The commander enters the preferred outcome, and the GA automatically evolves a battle plan; in the simulation used, factors such as the topography of the land, vegetative cover, troop movement speed, and firing accuracy were taken into account. In this experiment, co-evolution was also used to improve the quality of the solutions: battle plans for the enemy forces evolved concurrently with friendly plans, forcing the GA to correct any weaknesses in its own plan that an enemy could exploit. To measure the quality of solutions produced by the GA, they were compared to battle plans for the same scenario produced by a group of "experienced military experts... considered to be very capable of developing tactical courses of action for the size forces used in this experiment" (p.166). These seasoned experts both developed their own plan and, when the GA's solution was complete, were given a chance to examine it and modify it as they saw fit. Finally, all the sets of plans were run multiple times on the simulator to determine their average quality.
The results speak for themselves: the evolved solution outperformed both the military experts' own plan and the plan produced by their modifications to the GA's solution. "...[T]he plans produced by automated algorithms had a significantly higher mean performance than those generated by experienced military experts" (p.161). Furthermore, the authors note that the GA's plan made good tactical sense. (It involved a two-pronged attack on the enemy position by mechanized infantry platoons supported by attack helicopters and ground scouts, in conjunction with unmanned aerial vehicles conducting reconnaissance to direct artillery fire.) In addition, the evolved plan included individual friendly units performing doctrinal missions - an emergent property that appeared during the course of the run, rather than being specified by the experimenter. In increasingly networked modern battlefields, the attractive potential of an evolutionary algorithm that can automate the production of high-quality tactical plans should be obvious.
An interesting use of GAs in law enforcement was reported in Naik 1996, which described the "FacePrints" software, a project to help witnesses identify and describe criminal suspects. The cliched image of the police sketch artist drawing a picture of the suspect's face in response to witnesses' promptings is a difficult and inefficient method: most people are not good at describing individual aspects of a person's face, such as the size of the nose or shape of the jaw, but instead are better at recognizing whole faces. FacePrints takes advantage of this by using a genetic algorithm that evolves pictures of faces based on databases of hundreds of individual features that can be combined in a vast number of ways. The program shows randomly generated face images to witnesses, who pick the ones that most resemble the person they saw; the selected faces are then mutated and bred together to generate new combinations of features, and the process repeats until an accurate portrait of the suspect's face emerges. In one real-life robbery case, the final portraits created by the three witnesses were strikingly similar, and the resulting picture was printed in the local paper.
- Molecular biology
In living things, transmembrane proteins are proteins that protrude through a cellular membrane. Transmembrane proteins often perform important functions such as sensing the presence of certain substances outside the cell or transporting them into the cell. Understanding the behavior of a transmembrane protein requires identifying the segment of that protein that is actually embedded within the membrane, which is called the transmembrane domain. Over the last two decades, molecular biologists have published a succession of increasingly accurate algorithms for this purpose.
All proteins used by living things are made up of the same 20 amino acids. Some of these amino acids are hydrophobic, meaning they are repelled by water, and some are hydrophilic, meaning they are attracted to water. Amino acid sequences that are part of a transmembrane domain are more likely to be hydrophobic. However, hydrophobicity is not a precisely defined characteristic, and there is no one agreed-upon scale for measuring it.
Koza et al. 1999, chapter 16, used genetic programming to design an algorithm to identify transmembrane domains of a protein. Genetic programming was given a set of standard mathematical operators to work with, as well as a set of boolean amino-acid-detecting functions that return +1 if the amino acid at a given position is the amino acid they detect and otherwise return -1. (For example, the A? function takes as an argument one number corresponding to a position within the protein, and returns +1 if the amino acid at that position is alanine, which is denoted by the letter A; otherwise it returns -1). A single shared memory variable kept a running count of the overall sum, and when the algorithm completed, the protein segment was identified as a transmembrane domain if its value was positive. Given only these tools, would it entail the creation of new information for a human designer to produce an efficient solution to this problem?
The solutions produced by genetic programming were evaluated for fitness by testing them on 246 protein segments whose transmembrane status was known. The best-of-run individual was then evaluated on 250 additional, out-of-sample, test cases and compared to the performance of the four best known human-written algorithms for the same purpose. The result: Genetic programming produced a transmembrane segment-identifying algorithm with an overall error rate of 1.6% - significantly lower than all four human-written algorithms, the best of which had an error rate of 2.5%. The genetically designed algorithm, which the authors dubbed the 0-2-4 rule, operates as follows:
- Increment the running sum by 4 for each instance of glutamic acid (an electrically charged and highly hydrophilic) amino acid in the protein segment.
- Increment the running sum by 0 for each instance of alanine, phenylalanine, isoleucine, leucine, methionine, or valine (all highly hydrophobic amino acids) in the protein segment.
- Increment the running sum by 2 for each instance of all other amino acids.
- If [(SUM - 3.1544)/0.9357] is less than the length of the protein segment, classify that segment as a transmembrane domain; otherwise, classify it as a nontransmembrane domain.
- Pattern recognition and data mining
Competition in the telecommunications industry today is fierce, and a new term - "churn" - has been coined to describe the rapid rate at which subscribers switch from one service provider to another. Churn costs telecom carriers a large amount of money each year, and reducing churn is an important factor in increasing profitability. If carriers can contact customers who are likely to switch and offer them special incentives to stay, churn rates can be reduced; but no carrier has the resources to contact more than a small percent of its customers. The problem is therefore how to identify customers who are more likely to churn. All carriers have extensive databases of customer information that can theoretically be used for this purpose; but what method works best for sifting through this vast amount of data to identify the subtle patterns and trends that signify a customer's likelihood of churning?
Au, Chan and Yao 2003 applied genetic algorithms to this problem to generate a set of if-then rules that predict the churning probability of different groups of customers. In their GA, the first generation of rules, all of which had one condition, was generated using a probabilistic induction technique. Subsequent generations then refine these, combining simple, single-condition rules into more complex, multi-condition rules. The fitness measure used an objective "interestingness" measure of correlation which requires no subjective input. The evolutionary data-mining algorithm was tested on a real-world database of 100,000 subscribers provided by a Malaysian carrier, and its performance was compared against two alternative methods: a multilayer neural network and a widely used decision-tree-based algorithm, C4.5. The authors state that their EA was able to discover hidden regularities in the database and was "able to make accurate churn prediction under different churn rates" (p.542), outperforming C4.5 under all circumstances, outperforming the neural network under low monthly churn rates and matching the neural network under larger churn rates, and reaching conclusions more quickly in both cases. Some further advantages of the evolutionary approach are that it can operate efficiently even when some data fields are missing and that it can express its findings in easily understood rule sets, unlike the neural net.
Among some of the more interesting rules discovered by the EA are as follows: subscribers are more likely to churn if they are personally subscribed to the service plan and have not been admitted to any bonus scheme (a potential solution is to admit all such subscribers to bonus schemes); subscribers are more likely to churn if they live in Kuala Lumpur, are between 36 and 44 in age, and pay their bills with cash (presumably because it is easier for subscribers who pay cash, rather than those whose accounts are automatically debited, to switch providers); and subscribers living in Penang who signed up through a certain dealer are more likely to churn (this dealer may be providing poor customer service and should be investigated).
Rizki, Zmuda and Tamburino 2002 used evolutionary algorithms to evolve a complex pattern recognition system with a wide variety of potential uses. The authors note that the task of pattern recognition is increasingly being performed by machine learning algorithms, evolutionary algorithms in particular. Most such approaches begin with a pool of predefined features, from which an EA can select appropriate combinations for the task at hand; by contrast, this approach began from the ground up, first evolving individual feature detectors in the form of expression trees, then evolving cooperative combinations of those detectors to produce a complete pattern recognition system. The evolutionary process automatically selects the number of feature detectors, the complexity of the detectors, and the specific aspects of the data each detector responds to.
To test their system, the authors gave it the task of classifying aircraft based on their radar reflections. The same kind of aircraft can return quite different signals depending on the angle and elevation at which it is viewed, and different kinds of aircraft can return very similar signals, so this is a non-trivial task. The evolved pattern recognition system correctly classified 97.2% of the targets, a higher net percentage than any of the three other techniques - a perceptron neural network, a nearest-neighbor classifier algorithm, and a radial basis algorithm - against which it was tested. (The radial basis network's accuracy was only 0.5% less than the evolved classifier, which is not a statistically significant difference, but the radial basis network required 256 feature detectors while the evolved recognition system used only 17.) As the authors state, "The recognition systems that evolve use fewer features than systems formed using conventional techniques, yet achieve comparable or superior recognition accuracy" (p.607). Various aspects of their system have also been applied to problems including optical character recognition, industrial inspection and medical image analysis.
Hughes and Leyland 2000 also applied multiple-objective GAs to the task of classifying targets based on their radar reflections. High-resolution radar cross section data requires massive amounts of disk storage space, and it is very computationally intensive to produce an actual model of the source from the data. By contrast, the authors' GA-based approach proved very successful, producing a model as good as the traditional iterative approach while reducing the computational overhead and storage requirements to the point where it was feasible to generate good models on a desktop computer. By contrast, the traditional iterative approach requires ten times the resolution and 560,000 times as many accesses of image data to produce models of similar quality. The authors conclude that their results "clearly demonstrate" (p.160) the ability of the GA to process both two- and three-dimensional radar data of any level of resolution with far fewer calculations than traditional methods, while retaining acceptably high accuracy.
- Robotics
The international RoboCup tournament is a project to promote advances in robotics, artificial intelligence, and related fields by providing a standard problem where new technologies can be tried out - specifically, it is an annual soccer tournament between teams of autonomous robots. (The stated goal is to develop a team of humanoid robots that can win against the world-champion human soccer team by 2050; at the present time, most of the competing robot teams are wheeled.) The programs that control the robotic team members must display complex behavior, deciding when to block, when to kick, how to move, when to pass the ball to teammates, how to coordinate defense and offense, and so on. In the simulator league of the 1997 competition, David Andre and Astro Teller entered a team named Darwin United whose control programs had been developed automatically from the ground up by genetic programming, a challenge to the conventional wisdom that "this problem is just too difficult for such a technique" (Andre and Teller 1999, p. 346).
To solve this difficult problem, Andre and Teller provided the genetic programming algorithm with a set of primitive control functions such as turning, moving, kicking, and so on. (These functions were themselves subject to change and refinement during the course of evolution.) Their fitness function, written to reward good play in general rather than scoring specifically, provided a list of increasingly important objectives: getting near the ball, kicking the ball, keeping the ball on the opponent's side of the field, moving in the correct direction, scoring goals, and winning the game. It should be noted that no code was provided to teach the team specifically how to achieve these complex objectives. The evolved programs were then evaluated using a hierarchical selection model: first, the candidate teams were tested on an empty field and rejected if they did not score a goal within 30 seconds. Next, they were evaluated against a team of stationary "kicking posts" that kick the ball toward the opposite side of the field. Thirdly, the team played a game against the winning team from the RoboCup 1997 competition. Finally, teams that scored at least one goal against this team were played off against each other to determine which was best.
Out of 34 teams in its division, Darwin United ultimately came in 17th, placing squarely in the middle of the field and outranking half of the human-written entries. While a tournament victory would undoubtedly have been more impressive, this result is competitive and significant in its own right, and appears even more so in the light of history. About 25 years ago, chess-playing computer programs were in their infancy; a computer had only recently entered even a regional competition for the first time, although it did not win (Sagan 1979, p.286). But "[a] machine that plays chess in the middle range of human expertise is a very capable machine" (ibid.), and it might be said that the same is true of robot soccer. Just as chess-playing machines compete at world grandmaster levels today, what types of systems will genetic programming be producing 20 or 30 years from now?
- Routing and scheduling
Burke and Newall 1999 used genetic algorithms to schedule exams among university students. The timetable problem in general is known to be NP-complete, meaning that no method is known to find a guaranteed-optimal solution in a reasonable amount of time. In such a problem, there are both hard constraints - two exams may not be assigned to the same room at the same time - and soft constraints - students should not be assigned to multiple exams in succession, if possible, to minimize fatigue. Hard constraints must be satisfied, while soft constraints should be satisfied as far as possible. The authors dub their hybrid approach for solving this problem a "memetic algorithm": an evolutionary algorithm with rank-based, fitness-proportionate selection, combined with a local hill-climber to optimize solutions found by the EA. The EA was applied to data sets from four real universities (the smallest of which had an enrollment of 25,000 students), and its results were compared to results produced by a heuristic backtracking method, a well-established algorithm that is among the best known for this problem and that is used at several real universities. Compared to this method, the EA produced a result with a quite uniform 40% reduction in penalty.
He and Mort 2000 applied genetic algorithms to the problem of finding optimal routing paths in telecommunications networks (such as phone networks and the Internet) which are used to relay data from senders to recipients. This is an NP-hard optimization problem, a type of problem for which GAs are "extremely well suited... and have found an enormous range of successful applications in such areas" (p.42). It is also a multiobjective problem, balancing conflicting objectives such as maximizing data throughput, minimizing transmission delay and data loss, finding low-cost paths, and distributing the load evenly among routers or switches in the network. Any successful real-world algorithm must also be able to re-route around primary paths that fail or become congested.
In the authors' hybrid GA, a shortest-path-first algorithm, which minimizes the number of "hops" a given data packet must pass through, is used to generate the seed for the initial population. However, this solution does not take into account link congestion or failure, which are inevitable conditions in real networks, and so the GA takes over, swapping and exchanging sections of paths. When tested on a data set derived from a real Oracle network database, the GA was found to be able to efficiently route around broken or congested links, balancing traffic load and maximizing the total network throughput. The authors state that these results demonstrate the "effectiveness and scalability" of the GA and show that "optimal or near-optimal solutions can be achieved" (p.49).
This technique has found real-world applications for similar purposes, as reported in Begley and Beals 1995. The telecommunications company U.S. West (now merged with Qwest) was faced with the task of laying a network of fiber-optic cable. Until recently, the problem of designing the network to minimize the total length of cable laid was solved by an experienced engineer; now the company uses a genetic algorithm to perform the task automatically. The results: "Design time for new networks has fallen from two months to two days and saves US West $1 million to $10 million each" (p.70).
Jensen 2003 and Chryssolouris and Subramaniam 2001 applied genetic algorithms to the task of generating schedules for job shops. This is an NP-hard optimization problem with multiple criteria: factors such as cost, tardiness, and throughput must all be taken into account, and job schedules may have to be rearranged on the fly due to machine breakdowns, employee absences, delays in delivery of parts, and other complications, making robustness in a schedule an important consideration. Both papers concluded that GAs are significantly superior to commonly used dispatching rules, producing efficient schedules that can more easily handle delays and breakdowns. These results are not merely theoretical, but have been applied to real-world situations:
As reported in Naik 1996, organizers of the 1992 Paralympic Games used a GA to schedule events. As reported in Petzinger 1995, John Deere & Co. has used GAs to generate schedules for a Moline, Illinois plant that manufactures planters and other heavy agricultural equipment. Like luxury cars, these can be built in a wide variety of configurations with many different parts and options, and the vast number of possible ways to build them made efficient scheduling a seemingly intractable problem. Productivity was hampered by scheduling bottlenecks, worker teams were bickering, and money was being lost. Finally, in 1993, Deere turned to Bill Fulkerson, a staff analyst and engineer who conceived of using a genetic algorithm to produce schedules for the plant. Overcoming initial skepticism, the GA quickly proved itself: monthly output has risen by 50 percent, overtime has nearly vanished, and other Deere plants are incorporating GAs into their own scheduling.
As reported in Rao 1998, Volvo has used an evolutionary program called OptiFlex to schedule its million-square-foot factory in Dublin, Virginia, a task that requires handling hundreds of constraints and millions of possible permutations for each vehicle. Like all genetic algorithms, OptiFlex works by randomly combining different scheduling possibilities and variables, determines their fitness by ranking them according to costs, benefits and constraints, then causes the best solutions to swap genes and sends them back into the population for another trial. Until recently, this daunting task was handled by a human engineer who took up to four days to produce the schedule for each week; now, thanks to GAs, this task can be completed in one day with minimal human intervention.
As reported in Lemley 2001, United Distillers and Vintners, a Scottish company that is the largest and most profitable spirits distributor in the world and accounts for over one-third of global grain whiskey production, uses a genetic algorithm to manage its inventory and supply. This is a daunting task, requiring the efficient storage and distribution of over 7 million barrels containing 60 distinct recipes among a vast system of warehouses and distilleries, depending on a multitude of factors such as age, malt number, wood type and market conditions. Previously, coordinating this complex flow of supply and demand required five full-time employees. Today, a few keystrokes on a computer instruct a genetic algorithm to generate a new schedule each week, and warehouse efficiency has nearly doubled.
Beasley, Sonander and Havelock 2001 used a GA to schedule airport landings at London Heathrow, the United Kingdom's busiest airport. This is a multiobjective problem that involves, among other things, minimizing delays and maximizing number of flights while maintaining adequate separation distances between planes (air vortices that form in a plane's wake can be dangerous to another flying too closely behind). When compared to actual schedules from a busy period at the airport, the GA was able to reduce average wait time by 2-5%, equating to one to three extra flights taking off and landing per hour - a significant improvement. However, even greater improvements have been achieved: as reported in Wired 2002, major international airports and airlines such as Heathrow, Toronto, Sydney, Las Vegas, San Francisco, America West Airlines, AeroMexico, and Delta Airlines are using genetic algorithms to schedule takeoffs, landings, maintenance and other tasks, in the form of Ascent Technology's SmartAirport Operations Center software (see http://www.ascent.com/faq.html). Breeding and mutating solutions in the form of schedules that incorporate thousands of variables, "Ascent beats humans hands-down, raising productivity by up to 30 percent at every airport where it's been implemented."
- Systems engineering
Benini and Toffolo 2002 applied a genetic algorithm to the multi-objective task of designing wind turbines used to generate electric power. This design "is a complex procedure characterized by several trade-off decisions... The decision-making process is very difficult and the design trends are not uniquely established" (p.357); as a result, there are a number of different turbine types in existence today and no agreement on which, if any, is optimal. Mutually exclusive objectives such as maximum annual energy production and minimal cost of energy must be taken into account. In this paper, a multi-objective evolutionary algorithm was used to find the best trade-offs between these goals, constructing turbine blades with the optimal configuration of characteristics such as tip speed, hub/tip ratio, and chord and twist distribution. In the end, the GA was able to find solutions competitive with commercial designs, as well as more clearly elucidate the margins by which annual energy production can be improved without producing overly expensive designs.
Haas, Burnham and Mills 1997 used a multiobjective genetic algorithm to optimize the beam shape, orientation and intensity of X-ray emitters used in targeted radiotherapy to destroy cancerous tumors while sparing healthy tissue. (X-ray photons aimed at a tumor tend to be partially scattered by structures within the body, unintentionally damaging internal organs. The challenge is to minimize this effect while maximizing the radiation dose delivered to the tumor.) Using a rank-based fitness model, the researchers began with the solution produced by the conventional method, an iterative least-squares approach, and then used the GA to modify and improve it. By constructing a model of a human body and exposing it to the beam configuration evolved by the GA, they found good agreement between the predicted and actual distributions of radiation. The authors conclude that their results "show a sparing of [healthy organs] that could not be achieved using conventional techniques" (p.1745).
Lee and Zak 2002 used a genetic algorithm to evolve a set of rules to control an automotive anti-lock braking system. While the ability of antilock brake systems to reduce stopping distance and improve maneuverability has saved many lives, the performance of an ABS is dependent on road surface conditions: for example, an ABS controller that is optimized for dry asphalt will not work as well on wet or icy roads, and vice versa. In this paper, the authors propose a GA to fine-tune an ABS controller that can identify the road surface properties (by monitoring wheel slip and acceleration) and respond accordingly, delivering the appropriate amount of braking force to maximize the wheels' traction. In testing, the genetically tuned ABS "exhibits excellent tracking properties" (p.206) and was "far superior" (p.209) to two other methods of braking maneuvers, quickly finding new optimal values for wheel slip when the type of terrain changes beneath a moving car and reducing total stopping distance. "The lesson we learned from our experiment... is that a GA can help to fine-tune even a well-designed controller. In our case, we already had a good solution to the problem; yet, with the help of a GA, we were able to improve the control strategy significantly. In summary, it seems that it is worthwhile to try to apply a GA, even to a well-designed controller, because there is a good chance that one can find a better set of the controller settings using GAs" (p.211).
As cited in Schechter 2000, Dr. Peter Senecal of the University of Wisconsin used small-population genetic algorithms to improve the efficiency of diesel engines. These engines work by injecting fuel into a combustion chamber which is filled with extremely compressed and therefore extremely hot air, hot enough to cause the fuel to explode and drive a piston that produces the vehicle's motive force. This basic design has changed little since it was invented by Rudolf Diesel in 1893; although vast amounts of effort have been put into making improvements, this is a very difficult task to perform analytically because it requires precise knowledge of the turbulent behavior displayed by the fuel-air mixture and simultaneous variation of many interdependent parameters. Senecal's approach, however, eschewed the use of such problem-specific knowledge and instead worked by evolving parameters such as the pressure of the combustion chamber, the timing of the fuel injections and the amount of fuel in each injection. The result: the simulation produced an improved engine that consumed 15% less fuel than a normal diesel engine and produced one-third as much nitric oxide exhaust and half as much soot. Senecal's team then built a real diesel engine according to the specifications of the evolved solution and got the same results. Senecal is now moving on to evolving the geometry of the engine itself, hopefully producing even greater improvements.
As cited in Begley and Beals 1995, Texas Instruments used a genetic algorithm to optimize the layout of components on a computer chip, placing structures so as to minimize the overall area and create the smallest chip possible. Using a connection strategy that no human had thought of, the GA came up with a design that took 18% less space.
Finally, as cited in Ashley 1992, a proprietary software system known as Engineous that employs genetic algorithms is being used by companies in the aerospace, automotive, manufacturing, turbomachinery and electronics industries to design and improve engines, motors, turbines and other industrial devices. In the words of its creator, Dr. Siu Shing Tong, Engineous is "a master 'tweaker,' tirelessly trying out scores of 'what-if' scenarios until the best possible design emerges" (p.49). In one trial of the system, Engineous was able to produce a 0.92 percent increase in the efficiency of an experimental turbine in only one week, while ten weeks of work by a human designer produced only a 0.5 percent improvement.
Granted, Engineous does not rely solely on genetic algorithms; it also employs numerical optimization techniques and expert systems which use logical if-then rules to mimic the decision-making process of a human engineer. However, these techniques are heavily dependent on domain-specific knowledge, lack general applicability, and are prone to becoming trapped on local optima. By contrast, the use of genetic algorithms allows Engineous to explore regions of the search space that other methods miss.
Engineous has found widespread use in a variety of industries and problems. Most famously, it was used to improve the turbine power plant of the Boeing 777 airliner; as reported in Begley and Beals 1995, the genetically optimized design was almost 1% more fuel-efficient than previous engines, which in a field such as this is "a windfall". Engineous has also been used to optimize the configuration of industrial DC motors, hydroelectric generators and steam turbines, to plan out power grids, and to design superconducting generators and nuclear power plants for orbiting satellites. Rao 1998 also reports that NASA has used Engineous to optimize the design of a high-altitude airplane for sampling ozone depletion, which must be both light and efficient.
As one might expect, the real-world demonstration of the power of evolution that GAs represent has proven surprising and disconcerting for creationists, who have always claimed that only intelligent design, not random variation and selection, could have produced the information content and complexity of living things. They have therefore argued that the success of genetic algorithms does not allow us to infer anything about biological evolution. The criticisms of two anti-evolutionists, representing two different viewpoints, will be addressed: young-earth creationist Dr. Don Batten of Answers in Genesis, who has written an article entitled " Genetic algorithms -- do they show that evolution works?", and old-earth creationist and intelligent-design advocate Dr. William Dembski, whose recent book No Free Lunch (Dembski 2002) discusses this topic.
Don Batten
- Some traits in living things are qualitative, whereas GAs are always quantitative
Batten states that GAs must be quantitative, so that any improvement can be selected for. This is true. He then goes on to say, "Many biological traits are qualitative--it either works or it does not, so there is no step-wise means of getting from no function to the function." This assertion has not been demonstrated, however, and is not supported by evidence. Batten does not even attempt to give an example of a biological trait that either "works or does not" and thus cannot be built up in a stepwise fashion.
But even if he did offer such a trait, how could he possibly prove that there is no stepwise path to it? Even if we do not know of such a path, does it follow that there is none? Of course not. Batten is effectively claiming that if we do not understand how certain traits evolved, then it is impossible for those traits to have evolved - a classic example of the elementary logical fallacy of argument from ignorance. The search space of all possible variants of any given biological trait is enormous, and in most cases our knowledge subsumes only an infinitesimal fraction of the possibilities. There may well be numerous paths to a structure which we do not yet know about; there is no reason whatsoever to believe our current ignorance sets limits on our future progress. Indeed, history gives us reason to be confident: scientists have made enormous progress in explaining the evolution of many complex biological structures and systems, both macroscopic and microscopic (for example, see these pages on the evolution of complex molecular systems, "clock" genes, the woodpecker's tongue or the bombardier beetle). We are justified in believing it likely that the ones that have so far eluded us will also be made clear in the future.
In fact, GAs themselves give us an excellent reason to believe this. Many of the problems to which they have been applied are complex engineering and design issues where the solution was not known ahead of time and therefore the problem could not be "rigged" to aid the algorithm's success. If the creationists were correct, it would have been entirely reasonable to expect genetic algorithms to fail dismally time after time when applied to these problems, but instead, just the opposite has occurred: GAs have discovered powerful, high-quality solutions to difficult problems in a diverse variety of fields. This calls into serious question whether there even are any problems such as Batten describes, whose solutions are inaccessible to an evolutionary process.
- GAs select for one trait at a time, whereas living things are multidimensional
Batten states that in GAs, "A single trait is selected for, whereas any living thing is multidimensional", and asserts that in living things with hundreds of traits, "selection has to operate on all traits that affect survival", whereas "[a] GA will not work with three or four different objectives, or I dare say even just two."
This argument reveals Batten's profound ignorance of the relevant literature. Even a cursory survey of the work done on evolutionary algorithms (or a look at an earlier section of this essay) would have revealed that multiobjective genetic algorithms are a major, thriving area of research within the broader field of evolutionary computation and prevented him from making such an embarrassingly incorrect claim. There are journal articles, entire issues of prominent journals on evolutionary computation, entire conferences, and entire books on the topic of multiobjective GAs. Coello 2000 provides a very extensive survey, with five pages of references to papers on the use of multiobjective genetic algorithms in a broad range of fields; see also Fleming and Purshouse 2002; Hanne 2000; Zitzler and Thiele 1999; Fonseca and Fleming 1995; Srinivas and Deb 1994; Goldberg 1989, p.197. For some books and papers discussing the use of multiobjective GAs to solve specific problems, see: Obayashi et al. 2000; Sasaki et al. 2001; Benini and Toffolo 2002; Haas, Burnham and Mills 1997; Chryssolouris and Subramaniam 2001; Hughes and Leyland 2000; He and Mort 2000; Kewley and Embrechts 2002; Beasley, Sonander and Havelock 2001; Sato et al. 2002; Tang et al. 1996; Williams, Crossley and Lang 2001; Koza et al. 1999; Koza et al. 2003. For a comprehensive repository of citations on multiobjective GAs, see http://www.lania.mx/~ccoello/EMOO/.
- GAs do not allow the possibility of extinction or error catastrophe
Batten claims that, in GAs, "Something always survives to carry on the process", while this is not necessarily true in the real world - in short, GAs do not allow the possibility of extinction.
However, this is not true; extinction can occur. For example, some GAs use a model of selection called thresholding, in which individuals must have a fitness higher than some predetermined level to survive and reproduce (Haupt and Haupt 1998, p. 37). If no individual meets this standard in such a GA, the population can indeed go extinct. But even in GAs that do not use thresholding, states analogous to extinction can occur. If mutation rates are too high or selective pressures too strong, then a GA will never find a feasible solution. The population may become hopelessly scrambled as deleterious mutations building up faster than selection can remove them disrupt fitter candidates (error catastrophe), or it may thrash around helplessly, unable to achieve any gain in fitness large enough to be selected for. Just as in nature, there must be a balance or a solution will never be reached. The one advantage a programmer has in this respect is that, if this does happen, he can reload the program with different values - for population size, for mutation rate, for selection pressure - and start over again. Obviously this is not an option for living things. Batten says, "There is no rule in evolution that says that some organism(s) in the evolving population will remain viable no matter what mutations occur," but there is no such rule in genetic algorithms either.
Batten also states that "the GAs that I have looked at artificially preserve the best of the previous generation and protect it from mutations or recombination in case nothing better is produced in the next iteration". This criticism will be addressed in the next point.
- GAs ignore the cost of substitution
Batten's next claim is that GAs neglect "Haldane's Dilemma", which states that an allele which contributes less to an organism's fitness will take a correspondingly longer time to become fixated in a population. Obviously, what he is referring to is the elitist selection technique, which automatically selects the best candidate at each generation no matter how small its advantage over its competitors is. He is right to suggest that, in nature, very slight competitive advantages might take much longer to propagate. Genetic algorithms are not an exact model of biological evolution in this respect.
However, this is beside the point. Elitist selection is an idealization of biological evolution - a model of what would happen in nature if chance did not intervene from time to time. As Batten acknowledges, Haldane's dilemma does not state that a slightly advantageous mutation will never become fixed in a population; it states that it will take more time for it to do so. However, when computation time is at a premium or a GA researcher wishes to obtain a solution more quickly, it may be desirable to skip this process by implementing elitism. An important point is that elitism does not affect which mutations arise, merely makes certain the selection of the best ones that do arise. It would not matter what the strength of selection was if information-increasing mutations did not occur. In other words, elitism speeds up convergence once a good solution has been discovered - it does not bring about an outcome which would not otherwise have occurred. Therefore, if genetic algorithms with elitism can produce new information, then so can evolution in the wild.
Furthermore, not all GAs use elitist selection. Many do not, instead relying only on roulette-wheel selection and other stochastic sampling techniques, and yet these have been no less successful. For instance, Koza et al. 2003, p.8-9, gives examples of 36 instances where genetic programming has produced human-competitive results, including the automated recreation of 21 previously patented inventions (six of which were patented during or after 2000), 10 of which duplicate the functionality of the patent in a new way, and also including two patentable new inventions and five new algorithms that outperform any human-written algorithms for the same purpose. As Dr. Koza states in an earlier reference to the same work (1999, p.1070): "The elitist strategy is not used." Some other papers cited in this essay in which elitism is not used include: Robin et al. 2003; Rizki, Zmuda and Tamburino 2002; Chryssolouris and Subramaniam 2001; Burke and Newall 1999; Glen and Payne 1995; Au, Chan and Yao 2003; Jensen 2003; Kewley and Embrechts 2002; Williams, Crossley and Lang 2001; Mahfoud and Mani 1996. In each of these cases, without any mechanism to ensure that the best individuals were selected at each generation, without exempting these individuals from potentially detrimental random change, genetic algorithms still produce powerful, efficient, human-competitive results. This fact may be surprising to creationists such as Batten, but it is wholly expected by advocates of evolution.
- GAs ignore generation time constraints
This criticism is puzzling. Batten claims that a single generation in a GA can take microseconds, whereas a single generation in any living organism can take anywhere from minutes to years. This is true, but how it is supposed to bear on the validity of GAs as evidence for evolution is not explained. If a GA can generate new information, regardless of how long it takes, then surely evolution in the wild can do so as well; that GAs can indeed do so is all this essay intends to demonstrate. The only remaining issue would then be whether biological evolution has actually had enough time to cause significant change, and the answer to this question would be one for biologists, geologists and physicists, not computer programmers.
The answer these scientists have provided is fully in accord with evolutionary timescales, however. Numerous lines of independent evidence, including radiometric isochron dating, the cooling rates of white dwarfs, the nonexistence of isotopes with short halflives in nature, the recession rates of distant galaxies, and analysis of the cosmic microwave background radiation all converge on the same conclusion: an Earth and a universe many billions of years old, easily long enough for evolution to produce all the diversity of life we see today by all reasonable estimates.
- GAs employ unrealistically high rates of mutation and reproduction
Batten asserts, without providing any supporting evidence or citations, that GAs "commonly produce 100s or 1000s of 'offspring' per generation", a rate even bacteria, the fastest-reproducing biological organisms, cannot match.
This criticism misses the mark in several ways. First of all, if the metric being used is (as it should be) number of offspring per generation, rather than number of offspring per unit of absolute time, then there clearly are biological organisms that can reproduce at rates faster than that of bacteria and roughly equal to the rates Batten claims are unrealistic. For example, a single frog can lay thousands of eggs at a time, each of which has the potential to develop into an adult. Granted, most of these usually will not survive due to resource limitations and predation, but then most of the "offspring" in each generation of a GA will not go on either.
Secondly, and more importantly, a genetic algorithm working on solving a problem is not meant to represent a single organism. Instead, a genetic algorithm is more analogous to an entire population of organisms - after all, it is populations, not individuals, that evolve. Of course, it is eminently plausible for a whole population to collectively have hundreds or thousands of offspring per generation. (Creationist Walter ReMine makes this same mistake with regards to Dr. Richard Dawkins' "weasel" program. See this Post of the Month for more.)
Additionally, Batten says, the mutation rate is artificially high in GAs, whereas living organisms have error-checking machinery designed to limit the mutation rate to about 1 in 10 billion base pairs (though this is too small - the actual figure is closer to 1 in 1 billion. See Dawkins 1996, p.124). Now of course this is true. If GAs mutated at this rate, they would take far too long to solve real-world problems. Clearly, what should be considered relevant is the rate of mutation relative to the size of the genome. The mutation rate should be high enough to promote a sufficient amount of diversity in the population without overwhelming the individuals. An average human will possess between one and five mutations; this is not at all unrealistic for the offspring in a GA.
- GAs have artificially small genomes
Batten's argument that the genome of a genetic algorithm "is artificially small and only does one thing" is badly misguided. In the first place, as we have seen, it is not true that a GA only does one thing; there are many examples of genetic algorithms specifically designed to optimize many parameters simultaneously, often far more parameters simultaneously than a human designer ever could.
And how exactly does Batten quantify "artificially small"? Many evolutionary algorithms, such as John Koza's genetic programming, use variable-length encodings where the size of candidate solutions can grow arbitrarily large. Batten claims that even the simplest living organism has far more information in its genome than a GA has ever produced, but while organisms living today may have relatively large genomes, that is because much complexity has been gained over the course of billions of years of evolution. As the Probability of Abiogenesis article points out, there is good reason to believe that the earliest living organisms were very much simpler than any species currently extant - self-replicating molecules probably no longer than 30 or 40 subunits, which could easily be specified by the 1800 bits of information that Batten apparently concedes at least one GA has generated. Genetic algorithms are similarly a very new technique whose full potential has not yet been tapped; digital computers themselves are only a few decades old, and as Koza (2003, p. 25) points out, evolutionary computing techniques have been generating increasingly more substantial and complex results over the last 15 years, in synchrony with the ongoing rapid increase in computing power often referred to as "Moore's Law". Just as early life was very simple compared to what came after, today's genetic algorithms, despite the impressive results they have already produced, are likely to give rise to far greater things in the future.
- GAs ignore the possibility of mutation occurring throughout the genome
Batten apparently does not understand how genetic algorithms work, and he shows it by making this argument. He states that in real life, "mutations occur throughout the genome, not just in a gene or section that specifies a given trait". This is true, but when he says that the same is not true of GAs, he is wrong. Exactly like in living organisms, GAs permit mutation and recombination to occur anywhere in the genomes of their candidate solutions; exactly like in living organisms, GAs must weed out the deleterious changes while simultaneously selecting for the beneficial ones.
Batten goes on to claim that "the program itself is protected from mutations; only target sequences are mutated", and if the program itself were mutated it would soon crash. This criticism, however, is irrelevant. There is no reason why the governing program of a GA should be mutated. The program is not part of the genetic algorithm; the program is what supervises the genetic algorithm and mutates the candidate solutions, which are what the programmer is seeking to improve. The program running the GA is not analogous to the reproductive machinery of an organism, a comparison which Batten tries to make. Rather, it is analogous to the invariant natural laws that govern the environments in which living organisms live and reproduce, and these are neither expected to change nor need to be "protected" from it.
- GAs ignore problems of irreducible complexity
Using old-earth creationist Michael Behe's argument of "irreducible complexity", Batten argues, "Many biological traits require many different components to be present, functioning together, for the trait to exist at all," whereas this does not happen in GAs.
However, it is trivial to show that such a claim is false, as genetic algorithms have produced irreducibly complex systems. For example, the voice-recognition circuit Dr. Adrian Thompson evolved (Davidson 1997) is composed of 37 core logic gates. Five of them are not even connected to the rest of the circuit, yet all 37 are required for the circuit to work; if any of them are disconnected from their power supply, the entire system ceases to function. This fits Behe's definition of an irreducibly complex system and shows that an evolutionary process can produce such things.
It should be noted that this is the same argument as the first one, merely presented in different language, and thus the refutation is the same. Irreducible complexity is not a problem for evolution, whether that evolution is occurring in living beings in the wild or in silicon on a computer's processor chip.
- GAs ignore polygeny, pleiotropy, and other genetic complexity
Batten argues that GAs ignore issues of polygeny (the determination of one trait by multiple genes), pleiotropy (one gene affecting multiple traits), and dominant and recessive genes.
However, none of these claims are true. GAs do not ignore polygeny and pleiotropy: these properties are merely allowed to arise naturally rather than being deliberately coded in. It is obvious that in any complex interdependent system (i.e., a nonlinear system), the alteration or removal of one part will cause a ripple effect of changes throughout; thus GAs naturally incorporate polygeny and pleiotropy. "In the genetic algorithm literature, parameter interaction is called epistasis (a biological term for gene interaction). When there is little to no epistasis, minimum seeking algorithms [i.e., hill-climbers --A.M.] perform best. Genetic algorithms shine when the epistasis is medium to high..." (Haupt and Haupt 1998, p. 31, original emphasis).
Likewise, there are some genetic algorithm implementations that do have diploid chromosomes and dominant and recessive genes (Goldberg 1989, p.150; Mitchell 1996, p.22). However, those that do not are simply more like haploid organisms, such as bacteria, than they are like diploid organisms, such as human beings. Since (by certain measures) bacteria are among the most successful organisms on this planet, such GAs remain a good model of evolution.
- GAs do not have multiple reading frames
Batten discusses the existence of multiple reading frames in the genomes of some living things, in which the DNA sequences code for different functional proteins when read in different directions or with different starting offsets. He asserts that "Creating a GA to generate such information-dense coding would seem to be out of the question".
Such a challenge begs for an answer, and here it is: Soule and Ball 2001. In this paper, the authors present a genetic algorithm with multiple reading frames and dense coding, enabling it to store more information than the total length of its genome. Like the three-nucleotide codons that specify amino acids in the genomes of living organisms, this GA's codons were five-digit binary strings. Since the codons were five digits long, there were five different possible reading frames. The sequence 11111 serves as a "start" codon and 00000 as a "stop" codon; because the start and stop codons could occur anywhere in the genome, the length of each individual was variable. Regions of the chromosome which did not fall between start-stop pairs were ignored.
The GA was tested on four classic function maximization problems. "Initially, the majority of the bits do not participate in any gene, i.e., most of a chromosome is non-coding. Again this is because in the initial random individuals there are relatively few start-stop codon pairs. However, the number of bits that do not participate decreases extremely rapidly." During the course of the run, the GA can increase the effective length of its genome by introducing new start codons in different reading frames. By the end of the run, "the amount of overlap is quite high. Many bits are participating in several (and often all five) genes." On all test problems, the GA started, on average, with 5 variables specified; by the end of the run, that number had increased to an average of around 25.
In the test problems, the GA with multiple reading frames produced significantly better solutions than a standard GA on two out of the four problems and better average solutions on the remaining two. In one problem, the GA successfully compressed 625 total bits of information into a chromosome only 250 bits long by using alternative reading frames. The authors label this behavior "extremely sophisticated" and conclude that "These data show that a GA can successfully use reading frames despite the added complexity" and "It is clear that a GA can introduce new 'genes' as necessary to solve a given problem, even with the difficulties imposed by using start and stop codons and overlapping genes".
- GAs have preordained goals
Like several others, this objection shows that Batten does not fully understand what a genetic algorithm is and how it works. He argues that GAs, unlike evolution, have goals predetermined and specified at the outset, and as an example of this, offers Dr. Richard Dawkins' "weasel" program.
However, the weasel program is not a true genetic algorithm, and is not typical of genetic algorithms, for precisely that reason. It was not intended to demonstrate the problem-solving power of evolution. Instead, its only intent was to show the difference between single-step selection (the infamous "tornado blowing through a junkyard producing a 747") and cumulative, multi-step selection. It did have a specific goal predetermined at the outset. True genetic algorithms, however, do not.
In a broadly general sense, GAs do have a goal: namely, to find an acceptable solution to a given problem. In this same sense, evolution also has a goal: to produce organisms that are better adapted to their environment and thus experience greater reproductive success. But just as evolution is a process without specific goals, GAs do not specify at the outset how a given problem should be solved. The fitness function is merely set up to evaluate how well a candidate solution performs, without specifying any particular way it should work and without passing judgment on whatever way it does invent. The solution itself then emerges through a process of mutation and selection.
Batten's next statement shows clearly that he does not understand what a genetic algorithm is. He asserts that "Perhaps if the programmer could come up with a program that allowed anything to happen and then measured the survivability of the 'organisms', it might be getting closer to what evolution is supposed to do" - but that is exactly how genetic algorithms work. They randomly generate candidate solutions and randomly mutate them over many generations. No configuration is specified in advance; as Batten puts it, anything is allowed to happen. As John Koza (2003, p. 37) writes, uncannily echoing Batten's words: "An important feature... is that the selection [in genetic programming] is not greedy. Individuals that are known to be inferior will be selected to a certain degree. The best individual in the population is not guaranteed to be selected. Moreover, the worst individual in the population will not necessarily be excluded. Anything can happen and nothing is guaranteed." (An earlier section discussed this very point as one of a GA's strengths.) And yet, by applying a selective filter to these randomly mutating candidates, efficient, complex and powerful solutions to difficult problems arise, solutions that were not designed by any intelligence and that can often equal or outperform solutions that were designed by humans. Batten's blithe assertion that "Of course that is impossible" is squarely contradicted by reality.
- GAs do not actually generate new information
Batten's final criticism runs: "With a particular GA, we need to ask how much of the 'information' generated by the program is actually specified in the program, rather than being generated de novo." He charges that GAs often do nothing more than find the best way for certain modules to interact when both the modules themselves and the ways they can interact are specified ahead of time.
It is difficult to know what to make of this argument. Any imaginable problem - terms in a calculus equation, molecules in a cell, components of an engine, stocks on a financial market - can be expressed in terms of modules that interact in given ways. If all one has is unspecified modules that interact in unspecified ways, there is no problem to be solved. Does this mean that the solution to no problem requires the generation of new information?
In regards to Batten's criticism about information contained in the solution being prespecified in the problem, the best way to assuage his concerns is to point out the many examples in which GAs begin with randomly generated initial populations that are not in any way designed to help the GA solve the problem. Some such examples include: Graham-Rowe 2004; Davidson 1997; Assion et al. 1998; Giro, Cyrillo and Galvão 2002; Glen and Payne 1995; Chryssolouris and Subramaniam 2001; Williams, Crossley and Lang 2001; Robin et al. 2003; Andreou, Georgopoulos and Likothanassis 2002; Kewley and Embrechts 2002; Rizki, Zmuda and Tamburino 2002; and especially Koza et al. 1999 and Koza et al. 2003, which discuss the use of genetic programming to generate 36 human-competitive inventions in analog circuit design, molecular biology, algorithmics, industrial controller design, and other fields, all starting from populations of randomly generated initial candidates.
Granted, some GAs do begin with intelligently generated solutions which they then seek to improve, but this is irrelevant: in such cases the aim is not just to return the initially input solution, but to improve it by the production of new information. In any case, even if the initial situation is as Batten describes, finding the most efficient way a number of modules can interact under a given set of constraints can be a far from trivial task, and one whose solution involves a considerable amount of new information: scheduling at international airports, for example, or factory assembly lines, or distributing casks among warehouses and distilleries. Again, GAs have proven themselves effective at solving problems whose complexity would swamp any human. In light of the multiple innovations and unexpectedly effective solutions arising from GAs in many fields, Batten's claim that "The amount of new information generated (by a GA) is usually quite trivial" rings hollow indeed.
William Dembski
Old-earth creationist Dr. William Dembski's recent book, No Free Lunch: Why Specified Complexity Cannot Be Purchased Without Intelligence, is largely devoted to the topic of evolutionary algorithms and how they relate to biological evolution. In particular, Dembski's book is concerned with an elusive quality he calls "specified complexity," which he asserts is contained in abundance in living things, and which he further asserts evolutionary processes are incapable of generating, leaving "design" through unspecified mechanisms by an unidentified "intelligent designer" the only alternative. To bolster his case, Dembski appeals to a class of mathematical theorems known as the No Free Lunch theorems, which he claims prove that evolutionary algorithms, on the average, do no better than blind search.
Richard Wein has written an excellent and comprehensive rebuttal to Dembski, entitled Not a Free Lunch But a Box of Chocolates, and its points will not be reproduced here. I will instead focus on chapter 4 of Dembski's book, which deals in detail with genetic algorithms.
Dembski has one main argument against GAs, which is developed at length throughout this chapter. While he does not deny that they can produce impressive results - indeed, he says that there is something "oddly compelling and almost magical" (p.221) about the way GAs can find solutions that are unlike anything designed by human beings - he argues that their success is due to the specified complexity that is "smuggled into" them by their human designers and subsequently embodied in the solutions they produce. "In other words, all the specified complexity we get out of an evolutionary algorithm has first to be put into its construction and into the information that guides the algorithm. Evolutionary algorithms therefore do not generate or create specified complexity, but merely harness already existing specified complexity" (p.207).
The first problem evident in Dembski's argument is this. Although his chapter on evolutionary algorithms runs for approximately 50 pages, the first 30 of those pages discuss nothing but Dr. Richard Dawkins' "weasel" algorithm, which, as already discussed, is not a true genetic algorithm and is not representative of genetic algorithms. Dembski's other two examples - the crooked wire genetic antennas of Edward Altshuler and Derek Linden and the checkers-playing neural nets of Kumar Chellapilla and David Fogel - are only introduced within the last 10 pages of the chapter and are discussed for three pages, combined. This is a serious deficiency, considering that the "weasel" program is not representative of most work being done in the field of evolutionary computation; nevertheless, Dembski's arguments relating to it will be analyzed.
In regard to the weasel program, Dembski states that "Dawkins and fellow Darwinists use this example to illustrate the power of evolutionary algorithms" (p.182), and, again, "Darwinists... are quite taken with the METHINKS IT IS LIKE A WEASEL example and see it as illustrating the power of evolutionary algorithms to generate specified complexity" (p.183). This is a straw man of Dembski's creation (not least because Dawkins' book was written long before Dembski ever coined that term!). Here is what Dawkins really says about the purpose of his program:
"What matters is the difference between the time taken by cumulative selection, and the time which the same computer, working flat out at the same rate, would take to reach the target phrase if it were forced to use the other procedure of single-step selection: about a million million million million million years." (Dawkins 1996, p.49, emphasis original)
In other words, the weasel program was intended to demonstrate the difference between two different kinds of selection: single-step selection, where a complex result is produced by pure chance in a single leap, and cumulative selection, where a complex result is built up bit by bit via a filtering process that preferentially preserves improvements. It was never intended to be a simulation of evolution as a whole.
Single-step selection is the absurdly improbable process frequently attacked in creationist literature by comparing it to a tornado blowing through a junkyard producing a 747 airliner, or an explosion in a print shop producing a dictionary. Cumulative selection is what evolution actually uses. Using single-step selection to achieve a functional result of any significant complexity, one would have to wait, on average, many times the current age of the universe. Using cumulative selection, however, that same result can be reached in a comparatively very short length of time. Demonstrating this difference was the point of Dawkins' weasel program, and that was the only point of that program. In a footnote to this chapter, Dembski writes, "It is remarkable how Dawkins' example gets recycled without any indication of the fundamental difficulties that attend it" (p.230), but it is only misconceptions in the minds of creationists such as Dembski and Batten, who attack the weasel program for not demonstrating something it was never intended to demonstrate, that give rise to these "difficulties".
Unlike every example of evolutionary algorithms discussed in this essay, the weasel program does indeed have a single, prespecified outcome, and the quality of the solutions it generates is judged by explicitly comparing them to that prespecified outcome. Therefore, Dembski is quite correct when he says that the weasel program does not generate new information. However, he then makes a gigantic and completely unjustified leap when he extrapolates this conclusion to all evolutionary algorithms: "As the sole possibility that Dawkins' evolutionary algorithm can attain, the target sequence in fact has minimal complexity.... Evolutionary algorithms are therefore incapable of generating true complexity" (p.182). Even Dembski seems to recognize this when he writes: "...most evolutionary algorithms in the literature are programmed to search a space of possible solutions to a problem until they find an answer - not, as Dawkins does here, by explicitly programming the answer into them in advance" (p.182). But then, having given a perfectly good reason why the weasel program is not representative of GAs as a whole, he inexplicably goes on to make precisely that fallacious generalization!
In reality, the weasel program is significantly different from most genetic algorithms, and therefore Dembski's argument from analogy does not hold up. True evolutionary algorithms, such as the examples discussed in this essay, do not simply find their way back to solutions already discovered by other methods - instead, they are presented with problems where the optimal solution is not known in advance, and are asked to discover that solution on their own. Indeed, if genetic algorithms could do nothing more than rediscover solutions already programmed into them, what would be the point of using them? It would be an exercise in redundancy to do so. However, the widespread scientific (and commercial) interest in GAs shows that there is far more substance to them than the rather trivial example Dembski tries to reduce this entire field to.
Having set up and then knocked down this straw man, Dembski moves on to his next line of argument: that the specified complexity exhibited by the outcomes of more representative evolutionary algorithms has, like the weasel program, been "smuggled in" by the designers of the algorithm. "But invariably we find that when specified complexity seems to be generated for free, it has in fact been front-loaded, smuggled in, or hidden from view" (p.204). Dembski suggests that the most common "hiding place" of specified complexity is in the GA's fitness function. "What the [evolutionary algorithm] has done is take advantage of the specified complexity inherent in the fitness function and used it in searching for and then locating the target..." (p.194). Dembski goes on to argue that, before an EA can search a given fitness landscape for a solution, some mechanism must first be employed to select that fitness landscape from what he calls a phase space of all the possible fitness landscapes, and if that mechanism is likewise an evolutionary one, some other mechanism must first be employed to select its fitness function from an even larger phase space, and so on. Dembski concludes that the only way to stop this infinite regress is through intelligence, which he holds to have some irreducible, mysterious ability to select a fitness function from a given phase space without recourse to higher-order phase spaces. "There is only one known generator of specified complexity, and that is intelligence" (p.207).
Dembski is correct when he writes that the fitness function "guid[es] an evolutionary algorithm into the target" (p.192). However, he is incorrect in his claim that selecting the right fitness function is a process that requires the generation of even more specified complexity than the EA itself produces. As Koza (1999, p. 39) writes, the fitness function tells an evolutionary algorithm "what needs to be done", not "how to do it". Unlike the unrepresentative weasel program example, the fitness function of an EA typically does not specify any particular form that the solution should take, and therefore it cannot be said to contribute "specified complexity" to the evolved solution in any meaningful sense.
An example will illustrate the point in greater detail. Dembski claims that in Chellapilla and Fogel's checkers experiment, their choice to hold the winning criterion constant from game to game "inserted an enormous amount of specified complexity" (p.223). It is certainly true that the final product of this process displayed a great deal of specified complexity (however one chooses to define that term). But is it true that the chosen fitness measure contained just as much specified complexity? Here is what Chellapilla and Fogel actually say:
"To appreciate the level of play that has been achieved, it may be useful to consider the following thought experiment. Suppose you are asked to play a game on an eight-by-eight board of squares with alternating colors. There are 12 pieces on each side arranged in a specific manner to begin play. You are told the rules of how the pieces move (i.e., diagonally, forced jumps, kings) and that the piece differential is available as a feature. You are not, however, told whether or not this differential is favorable or unfavorable (there is a version of checkers termed 'suicide checkers,' where the object is to 'lose' as fast as possible) or if it is even valuable information. Most importantly, you are not told the object of the game. You simply make moves and at some point an external observer declares the game over. They do not, however, provide feedback on whether or not you won, lost, or drew. The only data you receive comes after a minimum of five such games and is offered in the form of an overall point score. Thus, you cannot know with certainty which games contributed to the overall result or to what degree. Your challenge is to induce the appropriate moves in each game based only on this coarse level of feedback." (Chellapilla and Fogel 2001, p.427)
It exceeds the bounds of the absurd for Dembski to claim that this fitness measure inserted an "enormous" amount of specified complexity. If a human being who had never heard of checkers was given the same information, and we returned several months later to discover that he had become an internationally ranked checkers expert, should we conclude that specified complexity has been generated?
Dembski states that to overturn his argument, "one must show that finding the information that guides an evolutionary algorithm to a target is substantially easier than finding the target directly through a blind search" (p.204). I contend that this is precisely the case. Intuitively, it should not be surprising that the fitness function contains less information than the evolved solution. This is precisely the reason why GAs have found such widespread use: it is easier (requires less information) to write a fitness function that measures how good a solution is, than to design a good solution from scratch.
In more informal terms, consider Dembski's two examples, the crooked-wire genetic antenna and the evolved checkers-playing neural network named Anaconda. It requires a great deal of detailed information about the game of checkers to come up with a winning strategy (consider Chinook and its enormous library of endgames). However, it does not require equally detailed information to recognize such a strategy when one sees it: all we need observe is that that strategy consistently defeats its opponents. Similarly, a person who knew nothing about how to design an antenna that radiates evenly over a hemispherical region in a given frequency range could still test such an antenna and verify that it works as intended. In both cases, determining what constitutes high fitness is far easier (requires less information) than figuring out how to achieve high fitness.
Granted, even though choosing a fitness function for a given problem requires less information than actually solving the problem defined by that fitness function, it does take some information to specify the fitness function in the first place, and it is a legitimate question to ask where this initial information comes from. Dembski may still ask about the origin of human intelligence that enables us to decide to solve one problem rather than another, or about the origin of the natural laws of the cosmos that make it possible for life to exist and flourish and for evolution to occur. These are valid questions, and Dembski is entitled to wonder about them. However, by this point - seemingly unnoticed by Dembski himself - he has now moved away from his initial argument. He is no longer claiming that evolution cannot happen; instead, he is essentially asking why we live in a universe where evolution can happen. In other words, what Dembski does not seem to realize is that the logical conclusion of his argument is theistic evolution. It is fully compatible with a God who (as many Christians, including evolutionary biologist Kenneth Miller, believe) used evolution as his creative tool, and set up the universe in such a way as to make it not just likely, but certain.
I will conclude by clearing up some additional, minor misconceptions in chapter 4 of No Free Lunch. For starters, although Dembski, unlike Batten, is clearly aware of the field of multiobjective optimization, he erroneously states that "until some form of univalence is achieved, optimization cannot begin" (p.186). This essay's discussion of multiple-objective genetic algorithms shows the error of this. Perhaps other design techniques have this restriction, but one of the virtues of GAs is precisely that they can make trade-offs and optimize several mutually exclusive objectives simultaneously, and the human overseers can then pick whichever solution best achieves their goals from the final group of Pareto-optimal solutions. No method of combining multiple criteria into one is necessary.
Dembski also states that GAs "seem less adept at constructing integrated systems that require multiple parts to achieve novel functions" (p.237). The many examples detailed in this essay (particularly John Koza's use of genetic programming to engineer complex analog circuits) show this claim to be false as well.
Finally, Dembski mentions that INFORMS, the professional organization of the operations research community, pays very little attention to GAs, and this "is reason to be skeptical of the technique's general scope and power" (p.237). However, just because a particular scientific society is not making widespread use of GAs does not mean that such uses are not widespread elsewhere or in general, and this essay has endeavored to show that this is in fact the case. Evolutionary techniques have found a wide variety of uses in virtually any field of science one would care to name, as well as among many companies in the commercial sector. Here is a partial list:
By contrast, given the dearth of scientific discoveries and research stimulated by intelligent design, Dembski is in a poor position to complain about lack of practical application. Intelligent design is a vacuous hypothesis, telling us nothing more than "Some designer did something, somehow, at some time, to cause this result." By contrast, this essay has hopefully demonstrated that evolution is a problem-solving strategy rich with practical applications.
Even creationists find it impossible to deny that the combination of mutation and natural selection can produce adaptation. Nevertheless, they still attempt to justify their rejection of evolution by dividing the evolutionary process into two categories - "microevolution" and "macroevolution" - and arguing that only the second is controversial, and that any evolutionary change we observe is only an example of the first.
Now, microevolution and macroevolution are terms that have meaning to biologists; they are defined, respectively, as evolution below the species level and evolution at or above the species level. But the crucial difference between the way creationists use these terms and the way scientists use them is that scientists recognize that these two are fundamentally the same process with the same mechanisms, merely operating at different scales. Creationists, however, are forced to postulate some type of unbridgeable gap separating the two, in order for them to deny that the processes of change and adaptation we see operating in the present can be extrapolated to produce all the diversity observed in the living world.
However, genetic algorithms make this view untenable by demonstrating the fundamental seamlessness of the evolutionary process. Take, for example, a problem that consists of programming a circuit to discriminate between a 1-kilohertz and a 10-kilohertz tone, and respond respectively with steady outputs of 0 and 5 volts. Say we have a candidate solution that can accurately discriminate between the two tones, but its outputs are not quite steady as required; they produce small waveforms rather than the requisite unchanging voltage. Presumably, according to the creationist view, to change this circuit from its present state to the perfect solution would be "microevolution", a small change within the ability of mutation and selection to produce. But surely, a creationist would argue, to arrive at this same final state from a completely random initial arrangement of components would be "macroevolution" and beyond the reach of an evolutionary process. However, genetic algorithms were able to accomplish both, evolving the system from a random arrangement to the near-perfect solution and finally to the perfect, optimal solution. At no step of the way did an insoluble difficulty or a gap that could not be bridged turn up. At no point whatsoever was human intervention required to assemble an irreducibly complex core of components (despite the fact that the finished product does contain such a thing) or to "guide" the evolving system over a difficult peak. The circuit evolved, without any intelligent guidance, from a completely random and non-functional state to a tightly complex, efficient and optimal state. How can this not be a compelling experimental demonstration of the power of evolution?
It has been said that human cultural evolution has superceded the biological kind - that we as a species have reached a point where we are able to consciously control our society, our environment and even our genes to a sufficient degree to make the evolutionary process irrelevant. It has been said that the cultural whims of our rapidly changing society, rather than the comparatively glacially slow pace of genetic mutation and natural selection, is what determines fitness today. In a sense, this may well be true.
But in another sense, nothing could be further from the truth. Evolution is a problem-solving process whose power we are only beginning to understand and exploit; despite this, it is already at work all around us, shaping our technology and improving our lives, and in the future, these uses will only multiply. Without a detailed understanding of the evolutionary process, none of the countless advances we owe to genetic algorithms would have been possible. There is a lesson here to those who deny the power of evolution, as well as those who deny that knowledge of it has any practical benefit. As incredible as it may seem, evolution works. As the poet Lord Byron put it: "'Tis strange but true; for truth is always strange, stranger than fiction."
"Adaptive Learning: Fly the Brainy Skies." Wired, vol.10, no.3 (March 2002). Available online at http://www.wired.com/wired/archive/10.03/everywhere.html?pg=2.
Altshuler, Edward and Derek Linden. "Design of a wire antenna using a genetic algorithm." Journal of Electronic Defense, vol.20, no.7, p.50-52 (July 1997).Andre, David and Astro Teller. "Evolving team Darwin United." In RoboCup-98: Robot Soccer World Cup II, Minoru Asada and Hiroaki Kitano (eds). Lecture Notes in Computer Science, vol.1604, p.346-352. Springer-Verlag, 1999.
Andreou, Andreas, Efstratios Georgopoulos and Spiridon Likothanassis. "Exchange-rates forecasting: A hybrid algorithm based on genetically optimized adaptive neural networks." Computational Economics, vol.20, no.3, p.191-210 (December 2002).
Ashley, Steven. "Engineous explores the design space." Mechanical Engineering, February 1992, p.49-52.
Assion, A., T. Baumert, M. Bergt, T. Brixner, B. Kiefer, V. Seyfried, M. Strehle and G. Gerber. "Control of chemical reactions by feedback-optimized phase-shaped femtosecond laser pulses." Science, vol.282, p.919-922 (30 October 1998).
Au, Wai-Ho, Keith Chan, and Xin Yao. "A novel evolutionary data mining algorithm with applications to churn prediction." IEEE Transactions on Evolutionary Computation, vol.7, no.6, p.532-545 (December 2003).
Beasley, J.E., J. Sonander and P. Havelock. "Scheduling aircraft landings at London Heathrow using a population heuristic." Journal of the Operational Research Society, vol.52, no.5, p.483-493 (May 2001).
Begley, Sharon and Gregory Beals. "Software au naturel." Newsweek, May 8, 1995, p.70.
Benini, Ernesto and Andrea Toffolo. "Optimal design of horizontal-axis wind turbines using blade-element theory and evolutionary computation." Journal of Solar Energy Engineering, vol.124, no.4, p.357-363 (November 2002).
Burke, E.K. and J.P. Newall. "A multistage evolutionary algorithm for the timetable problem." IEEE Transactions on Evolutionary Computation, vol.3, no.1, p.63-74 (April 1999).
Charbonneau, Paul. "Genetic algorithms in astronomy and astrophysics." The Astrophysical Journal Supplement Series, vol.101, p.309-334 (December 1995).
Chellapilla, Kumar and David Fogel. "Evolving an expert checkers playing program without using human expertise." IEEE Transactions on Evolutionary Computation, vol.5, no.4, p.422-428 (August 2001). Available online at http://www.natural-selection.com/NSIPublicationsOnline.htm.
Chellapilla, Kumar and David Fogel. "Anaconda defeats Hoyle 6-0: a case study competing an evolved checkers program against commercially available software." In Proceedings of the 2000 Congress on Evolutionary Computation, p.857-863. IEEE Press, 2000. Available online at http://www.natural-selection.com/NSIPublicationsOnline.htm.
Chellapilla, Kumar and David Fogel. "Verifying Anaconda's expert rating by competing against Chinook: experiments in co-evolving a neural checkers player." Neurocomputing, vol.42, no.1-4, p.69-86 (January 2002).
Chryssolouris, George and Velusamy Subramaniam. "Dynamic scheduling of manufacturing job shops using genetic algorithms." Journal of Intelligent Manufacturing, vol.12, no.3, p.281-293 (June 2001).
Coale, Kristi. "Darwin in a box." Wired News, July 14, 1997. Available online at http://www.wired.com/news/technology/0,1282,5152,00.html.
Coello, Carlos. "An updated survey of GA-based multiobjective optimization techniques." ACM Computing Surveys, vol.32, no.2, p.109-143 (June 2000).
Davidson, Clive. "Creatures from primordial silicon." New Scientist, vol.156, no.2108, p.30-35 (November 15, 1997). Available online at http://www.newscientist.com/hottopics/ai/primordial.jsp.
Dawkins, Richard. The Blind Watchmaker: Why the Evidence of Evolution Reveals a Universe Without Design. W.W. Norton, 1996.
Dembski, William. No Free Lunch: Why Specified Complexity Cannot Be Purchased Without Intelligence. Rowman & Littlefield, 2002.
Fleming, Peter and R.C. Purshouse. "Evolutionary algorithms in control systems engineering: a survey." Control Engineering Practice, vol.10, p.1223-1241 (2002).Fonseca, Carlos and Peter Fleming. "An overview of evolutionary algorithms in multiobjective optimization." Evolutionary Computation, vol.3, no.1, p.1-16 (1995).
Forrest, Stephanie. "Genetic algorithms: principles of natural selection applied to computation." Science, vol.261, p.872-878 (1993).
Gibbs, W. Wayt. "Programming with primordial ooze." Scientific American, October 1996, p.48-50.
Gillet, Valerie. "Reactant- and product-based approaches to the design of combinatorial libraries." Journal of Computer-Aided Molecular Design, vol.16, p.371-380 (2002).
Giro, R., M. Cyrillo and D.S. Galvão. "Designing conducting polymers using genetic algorithms." Chemical Physics Letters, vol.366, no.1-2, p.170-175 (November 25, 2002).
Glen, R.C. and A.W.R. Payne. "A genetic algorithm for the automated generation of molecules within constraints." Journal of Computer-Aided Molecular Design, vol.9, p.181-202 (1995).
Goldberg, David. Genetic Algorithms in Search, Optimization, and Machine Learning. Addison-Wesley, 1989.
Graham-Rowe, Duncan. "Radio emerges from the electronic soup." New Scientist, vol.175, no.2358, p.19 (August 31, 2002). Available online at http://www.newscientist.com/news/news.jsp?id=ns99992732.
- See also: Bird, Jon and Paul Layzell. "The evolved radio and its implications for modelling the evolution of novel sensors." In Proceedings of the 2002 Congress on Evolutionary Computation, p.1836-1841.
Graham-Rowe, Duncan. "Electronic circuit 'evolves' from liquid crystals." New Scientist, vol.181, no.2440, p.21 (March 27, 2004).
Haas, O.C.L., K.J. Burnham and J.A. Mills. "On improving physical selectivity in the treatment of cancer: A systems modelling and optimisation approach." Control Engineering Practice, vol.5, no.12, p.1739-1745 (December 1997).
Hanne, Thomas. "Global multiobjective optimization using evolutionary algorithms." Journal of Heuristics, vol.6, no.3, p.347-360 (August 2000).
Haupt, Randy and Sue Ellen Haupt. Practical Genetic Algorithms. John Wiley & Sons, 1998.
He, L. and N. Mort. "Hybrid genetic algorithms for telecommunications network back-up routeing." BT Technology Journal, vol.18, no.4, p. 42-50 (Oct 2000).
Holland, John. "Genetic algorithms." Scientific American, July 1992, p. 66-72.
Hughes, Evan and Maurice Leyland. "Using multiple genetic algorithms to generate radar point-scatterer models." IEEE Transactions on Evolutionary Computation, vol.4, no.2, p.147-163 (July 2000).
Jensen, Mikkel. "Generating robust and flexible job shop schedules using genetic algorithms." IEEE Transactions on Evolutionary Computation, vol.7, no.3, p.275-288 (June 2003).
Kewley, Robert and Mark Embrechts. "Computational military tactical planning system." IEEE Transactions on Systems, Man and Cybernetics, Part C - Applications and Reviews, vol.32, no.2, p.161-171 (May 2002).
Kirkpatrick, S., C.D. Gelatt and M.P. Vecchi. "Optimization by simulated annealing." Science, vol.220, p.671-678 (1983).
Koza, John, Forest Bennett, David Andre and Martin Keane. Genetic Programming III: Darwinian Invention and Problem Solving. Morgan Kaufmann Publishers, 1999.Koza, John, Martin Keane, Matthew Streeter, William Mydlowec, Jessen Yu and Guido Lanza. Genetic Programming IV: Routine Human-Competitive Machine Intelligence. Kluwer Academic Publishers, 2003.
- See also: Koza, John, Martin Keane and Matthew Streeter. "Evolving inventions." Scientific American, February 2003, p. 52-59.
Keane, A.J. and S.M. Brown. "The design of a satellite boom with enhanced vibration performance using genetic algorithm techniques." In Adaptive Computing in Engineering Design and Control '96 - Proceedings of the Second International Conference, I.C. Parmee (ed), p.107-113. University of Plymouth, 1996.
Lee, Yonggon and Stanislaw H. Zak. "Designing a genetic neural fuzzy antilock-brake-system controller." IEEE Transactions on Evolutionary Computation, vol.6, no.2, p.198-211 (April 2002).
Lemley, Brad. "Machines that think." Discover, January 2001, p.75-79.
Mahfoud, Sam and Ganesh Mani. "Financial forecasting using genetic algorithms." Applied Artificial Intelligence, vol.10, no.6, p.543-565 (1996).
Mitchell, Melanie. An Introduction to Genetic Algorithms. MIT Press, 1996.
Naik, Gautam. "Back to Darwin: In sunlight and cells, science seeks answers to high-tech puzzles." The Wall Street Journal, January 16, 1996, p. A1.
Obayashi, Shigeru, Daisuke Sasaki, Yukihiro Takeguchi, and Naoki Hirose. "Multiobjective evolutionary computation for supersonic wing-shape optimization." IEEE Transactions on Evolutionary Computation, vol.4, no.2, p.182-187 (July 2000).
Petzinger, Thomas. "At Deere they know a mad scientist may be a firm's biggest asset." The Wall Street Journal, July 14, 1995, p.B1.
Porto, Vincent, David Fogel and Lawrence Fogel. "Alternative neural network training methods." IEEE Expert, vol.10, no.3, p.16-22 (June 1995).
Rao, Srikumar. "Evolution at warp speed." Forbes, vol.161, no.1, p.82-83 (January 12, 1998).
Rizki, Mateen, Michael Zmuda and Louis Tamburino. "Evolving pattern recognition systems." IEEE Transactions on Evolutionary Computation, vol.6, no.6, p.594-609 (December 2002).
Robin, Franck, Andrea Orzati, Esteban Moreno, Otte Homan, and Werner Bachtold. "Simulation and evolutionary optimization of electron-beam lithography with genetic and simplex-downhill algorithms." IEEE Transactions on Evolutionary Computation, vol.7, no.1, p.69-82 (February 2003).
Sagan, Carl. Broca's Brain: Reflections on the Romance of Science. Ballantine, 1979.
Sambridge, Malcolm and Kerry Gallagher. "Earthquake hypocenter location using genetic algorithms." Bulletin of the Seismological Society of America, vol.83, no.5, p.1467-1491 (October 1993).
Sasaki, Daisuke, Masashi Morikawa, Shigeru Obayashi and Kazuhiro Nakahashi. "Aerodynamic shape optimization of supersonic wings by adaptive range multiobjective genetic algorithms." In Evolutionary Multi-Criterion Optimization: First International Conference, EMO 2001, Zurich, Switzerland, March 2001: Proceedings, K. Deb, L. Theile, C. Coello, D. Corne and E. Zitler (eds). Lecture Notes in Computer Science, vol.1993, p.639-652. Springer-Verlag, 2001.
Sato, S., K. Otori, A. Takizawa, H. Sakai, Y. Ando and H. Kawamura. "Applying genetic algorithms to the optimum design of a concert hall." Journal of Sound and Vibration, vol.258, no.3, p. 517-526 (2002).
Schechter, Bruce. "Putting a Darwinian spin on the diesel engine." The New York Times, September 19, 2000, p. F3.
Srinivas, N. and Kalyanmoy Deb. "Multiobjective optimization using nondominated sorting in genetic algorithms." Evolutionary Computation, vol.2, no.3, p.221-248 (Fall 1994).
Soule, Terrence and Amy Ball. "A genetic algorithm with multiple reading frames." In GECCO-2001: Proceedings of the Genetic and Evolutionary Computation Conference, Lee Spector and Eric Goodman (eds). Morgan Kaufmann, 2001. Available online at http://www.cs.uidaho.edu/~tsoule/research/papers.html.
Tang, K.S., K.F. Man, S. Kwong and Q. He. "Genetic algorithms and their applications." IEEE Signal Processing Magazine, vol.13, no.6, p.22-37 (November 1996).
Weismann, Dirk, Ulrich Hammel, and Thomas Bäck. "Robust design of multilayer optical coatings by means of evolutionary algorithms." IEEE Transactions on Evolutionary Computation, vol.2, no.4, p.162-167 (November 1998).
Williams, Edwin, William Crossley and Thomas Lang. "Average and maximum revisit time trade studies for satellite constellations using a multiobjective genetic algorithm." Journal of the Astronautical Sciences, vol.49, no.3, p.385-400 (July-September 2001).
Zitzler, Eckart and Lothar Thiele. "Multiobjective evolutionary algorithms: a comparative case study and the Strength Pareto approach." IEEE Transactions on Evolutionary Computation, vol.3, no.4, p.257-271 (November 1999).




















![[Figure1.4.1 (cartoon of vertebrate jaws)]](http://www.talkorigins.org/faqs/comdesc/images/jaws2.gif)
![[Figure1.4.2a (cartoon of vertebrate ears)]](http://www.talkorigins.org/faqs/comdesc/images/reptile_ear.gif)
![[Figure1.4.2b (cartoon of vertebrate ears)]](http://www.talkorigins.org/faqs/comdesc/images/human_ear.gif)
![[Figure1.4.3 (cartoon of vertebrate jaws)]](http://www.talkorigins.org/faqs/comdesc/images/jaws1.gif)
![[Fig. 1a]](http://www.gcssepm.org/images/fossil_a.gif)
![[Fig. 1b]](http://www.gcssepm.org/images/fossil_b.gif)






