
Tonight my daughter was showing me a number line technique for determining if fractions are equal, or if one is greater than the other.
As far as I'm concerned the technique is faulty for several reasons. I'll post those after a few Freepers comment.
Why are meters different for boys and girls?
I’m just confused as to which length is a meter. I don’t know that it matters, but the different lengths might confuse a fifth grader.
White men can’t jump [as far as white girls].
The differing scales are misleading. Certainly 4/6 > 5/8.
Well, you don’t need more than 4th grade math in CA, anyway.
4/6 should be farther, but it looks like if you mark it the way they want you to, you’ll think 5/8 is farther.
It doesn’t require them to actually DO math.
Only to know how to count (and read).
Wow. Yank your kid out of public school.
And I support public schools - but my 4th grade daughter would laugh at this problem, as idiotic.

Both lines would have to be the same length before meaningful comparisons could be made between the eights and sixths - this looks like some sort of bizarre semi-psychotic PC scam to show that boys and girls both can jump the same distance even though the numbers seem to show they can’t.....
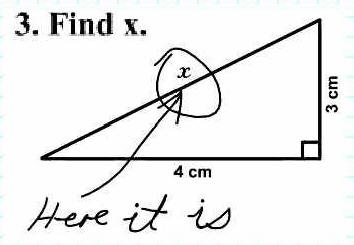
Just wait 'til they teach her geometry.
The lengths of those jumps should have been made in decimeters, centimeters or decimal fractions of a meter. The point of the metric system is to avoid those “messy” 3rds, 6ths, 8ths, etc!
Eagerly await your reasons for the faulty technique.
Another reason ping
We raised such a fuss about it they finally dropped them for this year.
Watch this video to see if this is what it is. Math Education: An Inconvenient Truth
I know it’s a math problem but I couldn’t help noticing that the word ‘further’ was used. Fail. Further denotes a degree, farther is used when refering to a distance.
Oh, and I see that all scaled are equal but some scales are more equal than others in CA.
I understand the point that was being attempted, but the problem is with the illustration. The two lines should be equal lengths with one being divided into 8 parts, the other into 6.
But 8/8 is not equal to 6/6 in the illustration.

Can someone explain to me why, according this graph, one meter equals 7/8 of a meter