The intent was not to provide a comprehensive overview of statistical mechanics, merely an introduction to the relation of entropy to statistical mechanics.
Are we assuming no internal degrees of freedom (monatomic gases)?
The author is merely assuming "air" and adds that it is a 'simple' example. While some elements of air are monatomic (ex noble gases), the other elements (obviously more) are diatomic elements hydrogen, nitrogen, oxygen etc...
"Entropy is a relationship between macroscopic and microscopic quantities. To illustrate what I mean by that statement I'm going to consider a simple example, namely a sealed room full of air. A full, microscopic description of the state of the room at any given time would include the position and velocity of every air molecule in it."
Wikipedia provides the example of a classical ideal diatomic gas.....
Do you happen to remember the term "partition function"?
The partition function is still a statement of probability that a system occupies or does not occupy a particular microstate
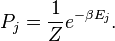
Thermodynamics can be used to describe the probability of a certain arrangements of entities compared to another, and which general direction those arrangments are most likely to move in without interference. While the definition of orderly is vague, it is clear there are orderly arrangments which we observe which it is absurd to assume that a natural process organized them. "a forest where all of the trees were equally spaced, you would probably conclude that the forest was man-made" or "leaves laid out in perfectly straight rows or in one neat pile. We can express the results of such observations by saying that a disorderly arrangement is much more probable then an orderly one if the laws of nature are allowed to act without interference." from the 3rd edition of this book (The edition I own)
There is an Organizer outside of nature who interfered when the world was created.