

Posted on 10/16/2010 8:13:34 AM PDT by tlb
Benoit B. Mandelbrot, a maverick mathematician who developed an innovative theory of roughness and applied it to physics, biology, finance and many other fields, died on Thursday in Cambridge, Mass. He was 85.
His death, at a hospice, was caused by pancreatic cancer, his wife, Aliette, said. He had lived in Cambridge.
Dr. Mandelbrot coined the term “fractal” to refer to a new class of mathematical shapes whose uneven contours could mimic the irregularities found in nature.
“Applied mathematics had been concentrating for a century on phenomena which were smooth, but many things were not like that: the more you blew them up with a microscope the more complexity you found,” said David Mumford, a professor of mathematics at Brown University.
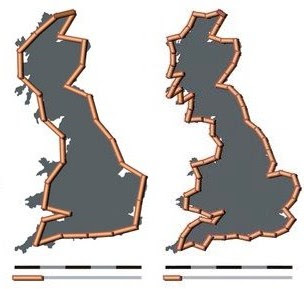
Dr. Mandelbrot traced his work on fractals to a question he first encountered as a young researcher: How long is the coast of Britain? The answer, he was surprised to discover, depends on how closely one looks. On a map an island may appear smooth, but zooming in will reveal jagged edges that add up to a longer coast. Zooming in further will reveal even more coastline.
“Here is a question, a staple of grade-school geometry that, if you think about it, is impossible,” Dr. Mandelbrot told The New York Times.
“The length of the coastline, in a sense, is infinite.”
“He doesn’t spend months or years proving what he has observed,” said Heinz Otto Peitgen, a professor of mathematics and biomedical sciences at the University of Bremen. And for that, he said, Dr. Mandelbrot “has received quite a bit of criticism.”
“But if we talk about impact inside mathematics, and applications in the sciences,” Professor Peitgen said, “he is one of the most important figures of the last 50 years.”
(Excerpt) Read more at nytimes.com ...
When fractal theory began to gain acceptance I had a small computer program that illustrated the principle. I spent quite a bit of time just watching the patterns develop.
Sad. In the whole, he is gone.
RIP - a true giant.
““The length of the coastline, in a sense, is infinite.””
I don’t get it. The length of a coastline if measured from the mean high tide could be measured to be a known quantity.
Is the infinite description a relative term based on observation from different perspectives?


What a great life. What a great mind.
Sad to see him go but he lived to see his work touch people’s lives almost every day in areas from cinema to finance and investing. His thoughts will influence mathematicians for centuries.
That is an elegant reply to the question in #4. Well done.
I was never close to him, but I assume he looked the same from any distance.
Thank you, I’m here all week! Try the veal!
BWAHAHAHAHAHAHA!
Funniest thing I’ve read in a long time.
It’s the same paradox as you see in the following anecdote:
If a rabbit hops halfway from his position to a carrot in one second, then half the remaining distance in the next second and half the remaining distance in the next, etc., how long will it take the rabbit to reach the carrot? Answer: forever. His velocity approaches zero since the distance he covers approaches zero while the time remains constant.
If you define the coastline down to the individual grains of sand on the beach and even beyond that, to the very atomic level, it can be argued that the distance approaches infinity. But of course that is absurd, since APPROACHING infinity is not the same as infinity. 10 ^^ x is a very large number, depending on x, but it is still not infinite.
The length of the coastline is proportional to the scale of the measurement.
If you measure in miles, you get one value.
If you measure in yards and convert that to miles, you get a larger value because the number of bumps and indentations in the coastline you can measure and don't have to average around is larger.
If you measure in inches and convert that to miles, you get a larger value still because you can now measure around every pebble and crack in the rock.
Take your measurements down to an infinitely small scale and you get an infinitely long coastline.
Or... Just see post 6.
:o)
Rest easy Dr. Mandelbrot.
It is hard to believe he's only 85, with all of the math theory he developed, explained and applied over the decades. Fractals are beautiful....they connect so much in the hypothetical and real world, and provide an underlying logic to almost everything that happens.
RIP, sir. You made a mark in history.

It was only until I was exposed to Mandelbrot’s approach to probability did I find an perspective that matched my own sympathies about randomness, especially in relationship to economics and financial markets. I never completed the dissertation that I started under him, but enjoyed the effort anyway.
No... I think it's infinite. Unless at some point nothing can ever get any smaller... which of course never happens. The rabbit can always go halfway, forever. He never reaches the carrot.
Formally, “In the limit of x approaching infinity, 10**x approaches infinity.”
I know it seems silly but there was a philosophical argument 200+ years ago on if man could understand infinity. It was decided that man can understand approaching infinity but not infinity.
Disclaimer: Opinions posted on Free Republic are those of the individual posters and do not necessarily represent the opinion of Free Republic or its management. All materials posted herein are protected by copyright law and the exemption for fair use of copyrighted works.