After 38 years, Israeli solves math code[Road Coloring Problem]

AP ^ | 20 Mar 2008 | ARON HELLER

[BGHater]

JERUSALEM - A mathematical puzzle that baffled the top minds in the esoteric field of symbolic dynamics for nearly four decades has been cracked — by a 63-year-old immigrant who once had to work as a security guard.

Avraham Trahtman, a mathematician who also toiled as a laborer after moving to Israel from Russia, succeeded where dozens failed, solving the elusive "Road Coloring Problem."

The conjecture essentially assumed it's possible to create a "universal map" that can direct people to arrive at a certain destination, at the same time, regardless of starting point. Experts say the proposition could have real-life applications in mapping and computer science.

The "Road Coloring Problem" was first posed in 1970 by Benjamin Weiss, an Israeli-American mathematician, and a colleague, Roy Adler, who worked at IBM at the time.

For eight years, Weiss tried to prove his theory. Over the next 30 years, some 100 other scientists attempted as well. All failed, until Trahtman came along and, in eight short pages, jotted the solution down in pencil last year.

"The solution is not that complicated. It's hard, but it is not that complicated," Trahtman said in heavily accented Hebrew. "Some people think they need to be complicated. I think they need to be nice and simple."

Weiss said it gave him great joy to see someone solve his problem.

Stuart Margolis, a mathematician who recruited Trahtman to teach at Bar Ilan University near Tel Aviv, called the solution one of the "beautiful results." But he said what makes the result especially remarkable is Trahtman's age and background.

"Math is usually a younger person's game, like music and the arts," Margolis said. "Usually you do your better work in your mid 20s and early 30s. He certainly came up with a good one at age 63."

Adding to the excitement is Trahtman's personal triumph in finally finding work as a mathematician after immigrating from Russia. "The first time I met him he was wearing a night watchman's uniform," Margolis said.

Originally from Yekaterinburg, Russia, Trahtman was an accomplished mathematician when he came to Israel in 1992, at age 48. But like many immigrants in the wave that followed the breakup of the Soviet Union, he struggled to find work in the Jewish state and was forced into stints working maintenance and security before landing a teaching position at Bar Ilan in 1995.

The soft-spoken Trahtman declined to talk about his odyssey, calling that the "old days." He said he felt "lucky" to be recognized for his solution, and played down the achievement as a "matter for mathematicians," saying it hasn't changed him a bit.

The puzzle tackled by Trahtman wasn't the longest-standing open problem to be solved recently. In 1994, British mathematician Andrew Wiles solved Fermat's last theorem, which had been open for more than 300 years.

Trahtman's solution is available on the Internet and is to be published soon in the Israel Journal of Mathematics.

Joel Friedman, a math professor at the University of British Columbia, said probably everyone in the field of symbolic dynamics had tried to solve the problem at some point, including himself. He said people in the related disciplines of graph theory, discrete math and theoretical computer science also tried.

"The solution to this problem has definitely generated excitement in the mathematical community," he said in an e-mail.

Margolis said the solution could have many applications.

"Say you've lost an e-mail and you want to get it back — it would be guaranteed," he said. "Let's say you are lost in a town you have never been in before and you have to get to a friend's house and there are no street signs — the directions will work no matter what."

___

On the Net:

Trahtman's solution: http://arxiv.org/abs/0709.0099

[BGHater]

Good stuff. We will be able to find missing socks. Amazing stuff, really.

[fso301]

The conjecture essentially assumed it's possible to create a "universal map" that can direct people to arrive at a certain destination, at the same time, regardless of starting point. Experts say the proposition could have real-life applications in mapping and computer science.

Think packet based communications.

[Squantos]

I was this close to solving this ..........:o)

[Hexenhammer]

I don't even understand the abstract of what they are talking about, but congratulations to him and his achievement regardless.

[nuconvert]

I always have trouble coloring when I’m the road

[CutePuppy]

Is it any similar to four-color maps?

[BGHater]

It’s all technicolor to me :)

[Doctor Don]

Guess you have to use the worm hole theory in this?

[Doctor Don]

Guess you have to use the worm hole theory in this?

[Squantos]

....... look at the special case of Road Coloring where at least one of the cities has an outgoing road ending in the same city. Suppose there are N cities, and Cx be any of the cities which have road to itself. We do the following visualization:

Keep Cx at the center and arrange the other cities in layers around it. First keep those cities which have roads directly leading to Cx to Cx in the first layer around Cx. Call this layer L1. Now keep the cities which have roads directly leading to cities of L1 in the next layer L2. Thus we keep all the cities in layers around Cx.

The coloring:
For every other city C, there is at least one outgoing road leading into the layer just inside of the layer on which C lies. Color this road from C to its next inner layer red. The other outgoing road from C is colored green. If both roads from C lead to the next inner layer, either may be colored red or green. For the central city Cx, the self-reaching loop road should be red.

With this coloring, one has a constant and finite path leading from ANY city to the central city Cx. This sequence of roads to the central city is always of the form of one Green followed by as many Reds as there are layers (an example is given below).

For any specified city C’, there exists a fixed path from central city Cx to it (guaranteed in problem statement). So given any destination C’, starting at any unknown source C, we can by first taking the constant path to the center and the path from center to C’. The path will be the same for any starting city C and will depend only on destination C’.

Example:

There are 5 cities numbered 1 to 5. arranged in a pentagon and connected clockwise. 1, 2, 4 and 5 have one road each that loops back on itself. 3-5 is another road.

ie, the roads are 1-2, 2-3, 3-4, 4-5, 5-1, 1-1, 2-2, 3-5, 4-4, 5-5

there are two cycles 1-2-3-5 (length 4) and 1-2-3-4-5 (length 5) - the lengths are relatively prime. As far as we can make out, this property is not used in what follows...

We choose 1 as the central city. The next layer has only 5 (since only from 5 is there a direct path to 1) In the next layer there are two cities, 3 and 4 In the outermost layer there is only 2.

By above coloring scheme, 2-3, 3-5, 4-5, 5-1, and 1-1 should be red and the others roads are green.

The seqeunce GRRR takes you to city 1 from any starting city. Once we have a samepath to the central city from anywhere we also have a same path to any required destination from anywhere.

[capydick]

No matter where you go....there you are.

[Ben Bolt]

Amazing stuff, really.

It is and a great find . Although I’ve not thought of other potential applications with this ,the story is tremendous .

This man seemingly went about his life just getting things done and never quitting . He stayed or is humble , could care less about getting anything for his contribution .

It’s a great human potential story with good examples of a serving heart . Excellent !

[colinhester]

Ping for later read...Thanks

[Conservative Infidel]

What... No pictures?

[Petronski]

Thank you. I now have a headache.

[ASOC]

I been outta school too long
“ Andrew Wiles solved Fermat’s last theorem”

I missed that completely. Now what is next - solving the unbounded discrepancy problem?

[ThomasThomas]

If everyone arrived at the same time from a trip then there would be long lines at the restrooms.

[LibFreeOrDie]

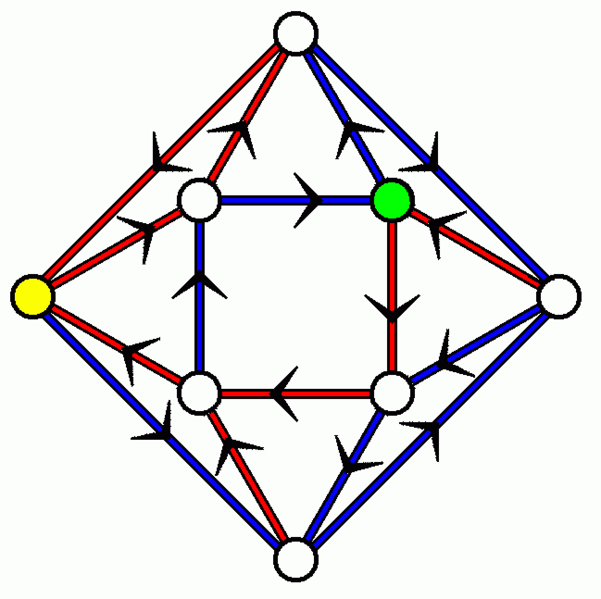
From Wikipedia:

The image [below] shows a directed graph on eight vertices in which each vertex has out-degree 2. (Each vertex in this case also has in-degree 2, but that is not necessary for a synchronizing coloring to exist.) The edges of this graph have been colored red and blue to create a synchronizing coloring.

For example, consider the vertex marked in yellow. No matter where in the graph you start, if you trace out the path "blue-red-red, blue-red-red, blue-red-red", you will end up at the yellow vertex. Similarly, if you trace out the path "blue-blue-red, blue-blue-red, blue-blue-red", you will always end up at the vertex marked in green, no matter where you started.

In the real world, this phenomenon would be as if you called a friend to ask for directions to his house, and he gave you a set of directions that worked no matter where you started from.

[spunkets]

"(since only from 5 is there a direct path to 1)"

There's trouble here young lad. Road 1-2 is missin' and ya gotta have it, 'er GRRR don't work. If ya find it, the oil cos. will be eternally grateful for all that drivin' around in circles ya caused.

[irishtenor]

I was there, once.