Skip to comments.
There Is No ‘Proper English’: Ignore grammar scolds. If people say it, it’s the right way to speak
Wall Street Journal ^
| 03/17/2015
| OLIVER KAMM
Posted on 03/17/2015 7:37:26 PM PDT by SeekAndFind
click here to read article
Navigation: use the links below to view more comments.
first previous 1-20 ... 81-100, 101-120, 121-140, 141-149 next last
To: FredZarguna
But even if we do think Leibniz was forging ahead of him on this account, surely Newton, who invented calculus out of his own head, was very sophisticated in his mathematical thinking. But how could this be possible if mathematics is a language in which he was not conversant?
I’m saying that the identification of mathematics with a certain style of language is an oversimplification, and a ham-handed one at that.
121
posted on
03/18/2015 9:02:40 PM PDT
by
dr_lew
To: FredZarguna
... and let me add. I recall reading somewhere some while ago, that Leibniz labored for a week or a month under the error of thinking that the differential of xy was dxdy.
What an absurd error! I recall this because at the time it gave me tremendous encouragement that Leibniz himself could have been so wrong. Now we regard it as a matter of "language" that d(xy) = xdy + ydx, and we kid ourselves that this understanding is somehow automatic.
Well, now I'm thinking, I sure hope this is true!
122
posted on
03/18/2015 9:22:37 PM PDT
by
dr_lew
To: dr_lew
The closest thing I can find to this is in the free Ebook ( available in its entirety for "review" ) of Cajori's History of Mathematics, transcribed here by me, "by hand" :
In a paper of July 11, 1677, Leibniz gave correct rules for the differentiation of sums, products, quotients, powers and roots. He had given the differentials of a few negative fractional powers, as early as November 1676, but had made some mistakes. For d sqrt(x) he had given the erroneous value 1/sqrt(x), and in another place the value -1/2 x-1/2; for d 1/x2 occurs in one place the wrong value, -2/x2, while a few lines lower is given -3/x4, its correct value.
!!!!!!!!!!!!!!!
I guess I'm not the only one around here who's confused! Check it yourself ( page 224 ) if you don't believe my transcription.
Of course, all of us here( cough cough ) learned in the cradle that d/dx 1/x2 = -2/x3 . Cajori seems to have quoted the correct value of d/dx 1/x3.
This could make sense if Cajori was trying to convey that the last formula represented a correct APPLICATION of the formula, d/dx xn = n xn-1, in that case with n=3 .
Well, I don't know if my memory is flawed, or if I read some flawed account, but here we see authoritative testimony that Leibniz did make errors in the evaluation of differentials.
Or maybe my recollection is of a true account, since there is nothing here to contradict the idea that such a lapse may have occurred at some earlier stage.
123
posted on
03/18/2015 10:51:56 PM PDT
by
dr_lew
To: dr_lew
There's no "identification of mathematics with a certain style of language." It is a language. Attempts to convert it to English are what's ham-handed: they are simply translations. And there are always things lost in the translation of a more expressive language to a less expressive one. One of the reasons there is so little progress in mathematics until the 18th century is the insistence of writing mathematical descriptions in the local vernacular.
124
posted on
03/19/2015 4:47:39 AM PDT
by
FredZarguna
(O, the tears of unfathomable sadness. Yummy. Yummy.)
To: FredZarguna
But Newton described his own thinking in almost personal terms, so that I find it easy to follow him in my own mind. I don’t see how you can aver that this was not mathematical thinking, or that it was somehow in some disguised language, which you are calling “mathematics”.
125
posted on
03/19/2015 3:27:03 PM PDT
by
dr_lew
To: dr_lew
English is simply not adequate to describe mathematical concepts. Arguing that it is denies the reality that nearly all growth in mathematics since Newton’s time involves terms, definitions, and symbols which are were not part of English while Newton lived. Had English been adequate to the purpose these extensions would not have been necessary. It wasn’t.
126
posted on
03/19/2015 3:42:30 PM PDT
by
FredZarguna
(O, the tears of unfathomable sadness. Yummy. Yummy.)
To: SeekAndFind
Tell this to someone wanting into a boardroom.
Or to someone wanting to work for the WSJ.
127
posted on
03/19/2015 3:43:57 PM PDT
by
combat_boots
(The Lion of Judah cometh. Hallelujah. Gloria Patri, Filio et Spiritui Sancto!)
To: FredZarguna
Sure, there are all kinds of specialized notations with rules for manipulating the terms, and these form a model of the subject. They are often referred to as “machinery” as well as language. MTW in GRAVITATION are big on this kind of stuff ... “The mathematical formalism for manipulating differential forms with ease, called ‘exterior calculus’ is summarized concisely in Box 4.1”.
Of course, there are many examples in mathematics of this kind of thing, but I really don’t understand how this equates to mathematics itself, in toto, being “a language”.
128
posted on
03/19/2015 4:54:43 PM PDT
by
dr_lew
To: KarlInOhio
I believe the two most beautiful things ever written are the King James Bible (1611) and the works of William Shakespeare (First Folio 1623), “the sublime summit of literature in English” in the words of Harold Bloom. It just doesn’t get any better. And here’s George Orwell on Elizabethan English as opposed to the modern stuff.
As an example, Orwell “translated” Ecclesiastes 9:11:
I returned and saw under the sun, that the race is not to the swift, nor the battle to the strong, neither yet bread to the wise, nor yet riches to men of understanding, nor yet favour to men of skill; but time and chance happeneth to them all.
— into “modern English of the worst sort”:
Objective consideration of contemporary phenomena compels the conclusion that success or failure in competitive activities exhibits no tendency to be commensurate with innate capacity, but that a considerable element of the unpredictable must invariably be taken into account.
Here’s a link to one of the greatest essays ever written:
http://en.wikipedia.org/wiki/Politics_and_the_English_Language#.22Translation.22_of_Ecclesiastes
129
posted on
03/19/2015 5:38:00 PM PDT
by
donaldo
To: JRandomFreeper
Latin was pretty math-like in High School. But it was ‘dead’. Then we read some actual writings from back in the time (Hannibal I think). Where it did not match the rules, we were told the writer had made mistakes.
Hebrew was ‘dead’ for a while, till about 1947. They established a committee to make up new words for new times; words like bulldozer, and electricity. They tried to keep the language ‘under control’. (I suspect to retain purity, respecting the Torah.) Committee got way behind. Don’t know what they are doing now.
Then there’s Legal Language. I cannot understand some of that stuff. Tried to read a bankruptcy letter. Normal English words, but mysterious meanings, seemingly contradictory if they made any sense at all.
My main gripes are subject-verb agreement and its - it’s.
These things bring me to a screeching halt when reading the newspaper; got to recognize the error and then can continue.
Spell checker lets a lot of errors get through (to, two, too and others). But they are humorous, not errors due to ignorance. Papers don’t seem to have time to proof read their own stuff.
130
posted on
03/20/2015 8:10:32 AM PDT
by
Scrambler Bob
(an icon of resistance within the oppressed patriots, who represent resilience in the face of SSV)
To: dr_lew
This discussion is going nowhere, so there ins't much point in continuing it.
Mathematics, not English, is the language of physics -- among many other sciences. Mathematical explanations translated into English are simply: 1) Methods for initiating those who do not yet have the necessary mathematical vocabulary into the correct conceptual arenas or 2) Oversimplifications [models] used to present mathematical concepts from other points of view in order to aid comprehension. But they are not the concepts themselves.
Sophisticated mathematicians [and physicists, and engineers, and others] who do not speak the same superficial language are nevertheless able to communicate essential truths to each other using mathematics. If that doesn't convince you that mathematics is a language quite distinct from your superficial birth language, really, nothing will.
131
posted on
03/20/2015 10:31:12 AM PDT
by
FredZarguna
(O, the tears of unfathomable sadness. Yummy. Yummy.)
To: dr_lew
Poor Leibniz. If he hadn't stolen the Calculus from someone else and then tried to claim it as his own invention, he might have had a better understanding of it.
But fortunately we can clear up his confusion easily, and no English is required. A very poor, hastily drawn sketch and a smartphone make the mathematical concept accessible to Deutschsprachigen everywhere [and anyone else who doesn't speak the language of Newton]:
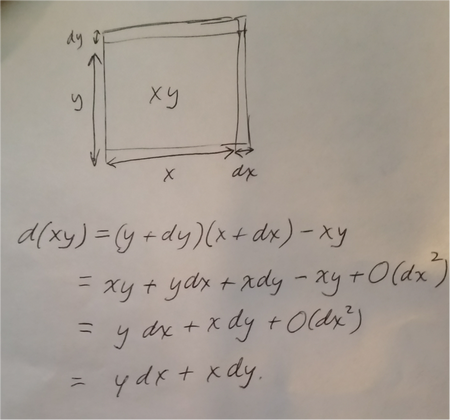
132
posted on
03/20/2015 11:04:18 AM PDT
by
FredZarguna
(O, the tears of unfathomable sadness. Yummy. Yummy.)
To: FredZarguna
But that O(dx
2) begs the question. It's a rote reminder that we have learned to discount this term, which is namely dxdy. The notation does not provide a justification for this, nor the means to do so.

133
posted on
03/20/2015 2:52:01 PM PDT
by
dr_lew
To: FredZarguna
Well I found a reference corroborating my recollection of Leibniz thinking d(xy) = dxdy. It's in "Huygens and Barrow, Newton and Hooke: Pioneers in Mathematical Analysis and ..." by Vladmir I. Arnold, on Google Books - $73.66 and up. Fortunately the "limited review" let me see the relevant page.
... he discovered that d(x+y) = dx+dy, and this remarkable discovery immediately forced him to think about what the differential of a product is. In accordance with the universality of his thoughts he rapidly came to the conclusion that differentiation is a ring homomorphism, that is, that the formula d(xy) = dxdy must hold.
He realized his error in short order and obtained the correct rule. Now see the irony here? He was thinking "linguistically", as you advocate, and the author ( V. Arnold ) notes that Newton et al would never have made this mistake since they were using physical reasoning, just as your diagram shows.
134
posted on
03/20/2015 6:15:13 PM PDT
by
dr_lew
To: dr_lew
It’s a lot of verbiage, and as Weierstrass and the truly rigorous mathematicians who followed him understood, it really mean nothing at all.
135
posted on
03/20/2015 7:21:57 PM PDT
by
FredZarguna
(It looks just like a Telefunken U-47 -- with leather.)
To: dr_lew
First of all, Leibniz had no concept of a ring homomorphism, which doesn't come into mathematics until nearly two hundred years after his death. Second, physical reasoning, useful as it is, isn't mathematical reasoning. Physicists have made great contributions to mathematics, but in the end they aren't mathematicians. Newton's arguments in the
Principia are regarded now as -- if anything -- quaint. But they aren't terribly persuasive, as your prior example shows.
Trying to make arguments that modern mathematical language isn't a language because most of it didn't exist three and a half centuries ago is as absurd as claiming you could post your missives with an abacus. That's roughly the width of the divide involved.
136
posted on
03/20/2015 7:35:00 PM PDT
by
FredZarguna
(It looks just like a Telefunken U-47 -- with leather.)
To: FredZarguna
It’s a lot of verbiage, and as Weierstrass and the truly rigorous mathematicians who followed him understood, it really mean nothing at all.That's absurd. It had some hidden limitations, which Weierstrass and others clarified, but these limitations are not evident in almost all cases of interest in applied mathematics.
Note that Newton was suspicious of "indivisibles" or infinitesimals, and is explaining why he used the more sound method of passing to a limit. I've got to ask, do you even comprehend this? I think I have the right to ask, since you claim it means nothing.
137
posted on
03/20/2015 8:09:07 PM PDT
by
dr_lew
To: dr_lew
“Passing to the limit” is simply hand-waving, which was not given rigorous mathematical soundness until Cauchy.
138
posted on
03/20/2015 8:13:31 PM PDT
by
FredZarguna
(It looks just like a Telefunken U-47 -- with leather.)
To: FredZarguna
Well, if this language that IS mathematics did not exist in the time of Euclid, then you’re saying that Euclid was not a mathematician. You’ve been implying as much with your disparaging remarks about Newton’s mathematics.
“mathematics” is from the Greek, you know. It means “learning”, and came to have the restricted meaining even in ancient times, since mathematical learning seemed to be the most elevated form of it.
139
posted on
03/20/2015 8:22:30 PM PDT
by
dr_lew
To: FredZarguna
First of all, Leibniz had no concept of a ring homomorphism, which doesn't come into mathematics until nearly two hundred years after his death. The author is giving this name to the analogy that Leibniz made. A ring is a structurally simple idea, and the nomenclature was a way of formalizing an existing concept.
I'm sure this was a bit of an extrapolation by the author, maybe even a bit of a joke.
140
posted on
03/20/2015 8:32:46 PM PDT
by
dr_lew
Navigation: use the links below to view more comments.
first previous 1-20 ... 81-100, 101-120, 121-140, 141-149 next last
Disclaimer:
Opinions posted on Free Republic are those of the individual
posters and do not necessarily represent the opinion of Free Republic or its
management. All materials posted herein are protected by copyright law and the
exemption for fair use of copyrighted works.
FreeRepublic.com is powered by software copyright 2000-2008 John Robinson